
【题目】如图,P为正方形ABCD的边BC上一动点(P与B、C不重合),连接AP,过点B作BQ⊥AP交CD于点Q,将△BQC沿BQ所在的直线对折得到△BQC′,延长QC′交BA的延长线于点M.
(1)试探究AP与BQ的数量关系,并证明你的结论;
(2)当AB=3,BP=2PC,求QM的长;
(3)当BP=m,PC=n时,求AM的长.

【答案】(1)AP=BQ;(2)QM的长为![]() ;(3)AM的长为
;(3)AM的长为![]() .
.
【解析】
(1)要证AP=BQ,只需证△PBA≌△QCB即可;
(2)过点Q作QH⊥AB于H,如图.易得QH=BC=AB=3,BP=2,PC=1,然后运用勾股定理可求得AP(即BQ)=![]() ,BH=2.易得DC∥AB,从而有∠CQB=∠QBA.由折叠可得∠C′QB=∠CQB,即可得到∠QBA=∠C′QB,即可得到MQ=MB.设QM=x,则有MB=x,MH=x-2.在Rt△MHQ中运用勾股定理就可解决问题;
,BH=2.易得DC∥AB,从而有∠CQB=∠QBA.由折叠可得∠C′QB=∠CQB,即可得到∠QBA=∠C′QB,即可得到MQ=MB.设QM=x,则有MB=x,MH=x-2.在Rt△MHQ中运用勾股定理就可解决问题;
(3)过点Q作QH⊥AB于H,如图,同(2)的方法求出QM的长,就可得到AM的长.
解:(1)AP=BQ.
理由:∵四边形ABCD是正方形,
∴AB=BC,∠ABC=∠C=90°,
∴∠ABQ+∠CBQ=90°.
∵BQ⊥AP,
∴∠PAB+∠QBA=90°,
∴∠PAB=∠CBQ.
在△PBA和△QCB中,
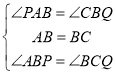 ,
,
∴△PBA≌△QCB,
∴AP=BQ;
(2)过点Q作QH⊥AB于H,如图.
∵四边形ABCD是正方形,
∴QH=BC=AB=3.
∵BP=2PC,
∴BP=2,PC=1,
∴BQ=AP=![]() =
=![]() =
=![]() ,
,
∴BH=![]() =
=![]() =2.
=2.
∵四边形ABCD是正方形,
∴DC∥AB,
∴∠CQB=∠QBA.
由折叠可得∠C′QB=∠CQB,
∴∠QBA=∠C′QB,
∴MQ=MB.
设QM=x,则有MB=x,MH=x-2.
在Rt△MHQ中,
根据勾股定理可得x2=(x-2)2+32,
解得x=![]() .
.
∴QM的长为![]() ;
;
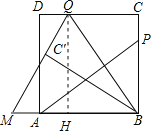
(3)过点Q作QH⊥AB于H,如图.
∵四边形ABCD是正方形,BP=m,PC=n,
∴QH=BC=AB=m+n.
∴BQ2=AP2=AB2+PB2,
∴BH2=BQ2-QH2=AB2+PB2-AB2=PB2,
∴BH=PB=m.
设QM=x,则有MB=QM=x,MH=x-m.
在Rt△MHQ中,
根据勾股定理可得x2=(x-m)2+(m+n)2,
解得x=m+n+![]() ,
,
∴AM=MB-AB=m+n+![]() -m-n=
-m-n=![]() .
.
∴AM的长为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,甲、乙两个可以自由转动的均匀的转盘,甲转盘被分成3个面积相等
的扇形,乙转盘被分成4个面积相等的扇形,每一个扇形都标有相应的数字,同时转
动两个转盘,当转盘停止后,设甲转盘中指针所指区域内的数字为m,乙转盘中指针
所指区域内的数字为n(若指针指在边界线上时,重转一次,直到指针都指向一个区
域为止).

【1】请你用画树状图或列表格的方法求出|m+n|>1的概率
【2】直接写出点(m,n)落在函数y=- 图象上的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知![]() ,
,![]() ,
,![]() 三点,其中a=
三点,其中a=![]() ,b,c满足关系式
,b,c满足关系式![]() ,P是第二象限内一点,连接PO,且P、A、C三点在一条直线上.
,P是第二象限内一点,连接PO,且P、A、C三点在一条直线上.
(1)求A、B、C三点的坐标;
(2)若规定:在三角形中,若两条边相等,则这两条边与第三边的夹角相等。如在△DEF中,DE=DF,则∠E=∠F.在本图中若PA=PO,AB=AC,CB⊥OB,垂足为B.求证:AB∥PO.
(3)如果在第二象限内有一点P(-2,![]() ),求四边形POBC的面积.
),求四边形POBC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,边长为6,D是BC边上的动点,∠EDF=60°.
(1)求证:△BDE∽△CFD;
(2)当BD=1,CF=3时,求BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(2,1),B(﹣1,1),C(﹣1,﹣3),D(2,﹣3),点P从点A出发,以每秒1个单位长度的速度沿A﹣B﹣C﹣D﹣A…的规律在图边形ABCD的边上循环运动,则第2019秒时点P的坐标为( )

A. (1,1)B. (0,1)C. (﹣1,1)D. (2,﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】六一期间,某公园游戏场举行“迎奥运”活动.有一种游戏的规则是:在一个装有![]() 个红球和若干个白球(每个球除颜色外其他相同)的袋中,随机摸一个球,摸到一个红球就得到一个奥运福娃玩具.已知参加这种游戏活动为
个红球和若干个白球(每个球除颜色外其他相同)的袋中,随机摸一个球,摸到一个红球就得到一个奥运福娃玩具.已知参加这种游戏活动为![]() 人次,公园游戏场发放的福娃玩具为
人次,公园游戏场发放的福娃玩具为![]() 个.
个.
![]() 求参加一次这种游戏活动得到福娃玩具的概率;
求参加一次这种游戏活动得到福娃玩具的概率;
![]() 请你估计袋中白球接近多少个?
请你估计袋中白球接近多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
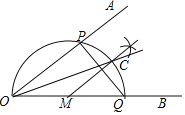
【题目】已知∠AOB,作图.
步骤1:在OB上任取一点M,以点M为圆心,MO长为半径画半圆,分别交OA、OB于点P、Q;
步骤2:过点M作PQ的垂线交弧PQ 于点C;
步骤3:画射线OC.
则下列判断:①弧CQ=弧PC;②MC∥OA;③OP=PQ;④OC平分∠AOB,
其中正确的为_______________(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB∥CD,AC平分∠BAD,CE∥AD交AB于E.

(1)求证:四边形AECD是菱形;
(2)若点E是AB的中点,试判断△ABC的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有A、B两组卡片共5张,A组的三张分别写有数字2,4,6,B组的两张分别写有3,5.它们除了数字外没有任何区别,
(1)随机从A组抽取一张,求抽到数字为2的概率;
(2)随机地分别从A组、B组各抽取一张,请你用列表或画树状图的方法表示所有等可能的结果.现制定这样一个游戏规则:若选出的两数之积为3的倍数,则甲获胜;否则乙获胜.请问这样的游戏规则对甲乙双方公平吗?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com