
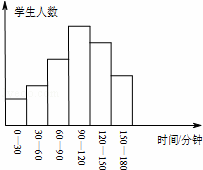
某记者抽样调查了某校一些学生假期用于读书的时间(单位:分钟)后,绘制了频数分布直方图,从左到右的前5个长方形相对应的频率之和为0.9,最后一组的频数是15,则此次抽样调查的人数为 150 人.(注:横轴上每组数据包含最小值不包含最大值)
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
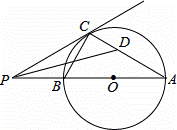
如图,AB是⊙O的直径,P为AB延长线上的一个动点,过点P作⊙O的切线,切点为C,连接AC,BC,作∠APC的平分线交AC于点D.
下列结论正确的是 (写出所有正确结论的序号)
①△CPD∽△DPA;
②若∠A=30°,则PC=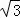 BC;
BC;
③若∠CPA=30°,则PB=OB;
④无论点P在AB延长线上的位置如何变化,∠CDP为定值.
查看答案和解析>>
科目:初中数学 来源: 题型:
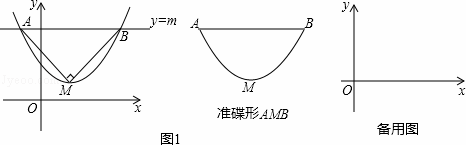
如图1,抛物线y=ax2+bx+c(a>0)的顶点为M,直线y=m与x轴平行,且与抛物线交于点A,B,若△AMB为等腰直角三角形,我们把抛物线上A,B两点之间的部分与线段AB围成的图形称为该抛物线对应的准蝶形,线段AB称为碟宽,顶点M称为碟顶,点M到线段AB的距离称为碟高.
(1)抛物线y=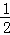 x2对应的碟宽
x2对应的碟宽 为 ;抛物线y=4x2对应的碟宽为 ;抛物线y=ax2(a>0)对应的碟宽为 ;抛物线y=a(x﹣2)2+3(a>0)对应的碟宽为 ;
为 ;抛物线y=4x2对应的碟宽为 ;抛物线y=ax2(a>0)对应的碟宽为 ;抛物线y=a(x﹣2)2+3(a>0)对应的碟宽为 ;
(2)抛物线y=ax2﹣4ax﹣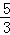 (a>0)对应的碟宽为6,且在x轴上,求a的值;
(a>0)对应的碟宽为6,且在x轴上,求a的值;
(3)将抛物线y=anx2+bnx+cn(an>0)的对应准蝶形记为Fn(n=1,2,3…),定义F1,F2,…,Fn为相似准蝶形,相应的碟宽之比即为相似比.若Fn与Fn﹣1的相似比为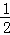 ,且Fn的碟顶是Fn﹣1的碟宽的中点,现将(2)中求得的抛物线记为y1,其对应的准蝶形记为F1.
,且Fn的碟顶是Fn﹣1的碟宽的中点,现将(2)中求得的抛物线记为y1,其对应的准蝶形记为F1.
①求抛物线y2的表达式;
②若F1的碟高为h1,F2的碟高为h2,…Fn的碟高为hn,则hn= ,Fn的碟宽有端点横坐标为 ;F1,F2,…,Fn的碟宽右端点是否在一条直线上?若是,直接写出该直线的表达式;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
某市出租车起步价是5元(3公里及3公里以内为起步价),以后每公里收费是1.6元,不足1公里按1公里收费,小明乘出租车到达目的地时计价器显示为11.4元,则此出租车行驶的路程可能为( )
|
| A. | 5.5公里 | B. | 6.9公里 | C. | 7.5公里 | D. | 8.1公里 |
查看答案和解析>>
科目:初中数学 来源: 题型:
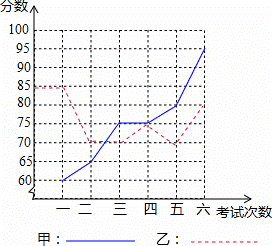
甲、乙两名同学进入初四后,某科6次考试成绩如图:
(1)请根据下图填写如表:
| 平均数 | 方差 | 中位数 | 众数 | 极差 | |
| 甲 | 75 |
| 75 |
|
|
| 乙 |
| 33.3 |
|
| 15 |
(2)请你分别从以下两个不同的方面对甲、乙两名同学6次考试成绩进行分析:
①从平均数和方差相结合看;②从折线图上两名同学分数的走势上看,你认为反映出什么问题?
查看答案和解析>>
科目:初中数学 来源: 题型:
某商场对上月笔袋销售的情况进行统计如下表所示:
| 颜色 | 白色 | 黄色 | 蓝色 | 紫色 | 红色 |
| 数量(个) | 56 | 128 | 520 | 210 | 16 |
经理决定本月进笔袋时多进一些蓝色的,经理的这一决定应用了哪个统计知识( )
|
| A. | 平均数 | B. | 方差 | C. | 中位数 | D. | 众数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com