
分析 (1)类比题干中乘方的运算即可得;
(2)类比题干中分数的乘方计算方法计算后即可得;
(3)根据(1)、(2)的规律即可得;
(4)逆用积的乘方将原式变形为($\frac{1}{2}$)-4×($\frac{3}{4}$)-4×($\frac{3}{4}$)4,再利用同底数幂进行计算可得.
解答 解:(1)∵($\frac{2}{3}$)2=$\frac{2}{3}$×$\frac{2}{3}$,($\frac{3}{2}$)-2=$\frac{1}{(\frac{3}{2})^{2}}$=$\frac{1}{\frac{3}{2}×\frac{3}{2}}$=$\frac{2}{3}$×$\frac{2}{3}$,
∴($\frac{2}{3}$)2=($\frac{3}{2}$)-2,
故答案为:=;
(2)∵($\frac{5}{4}$)3=$\frac{5}{4}$×$\frac{5}{4}$×$\frac{5}{4}$,($\frac{4}{5}$)-3=$\frac{1}{\frac{4}{5}×\frac{4}{5}×\frac{4}{5}}$=$\frac{5}{4}$×$\frac{5}{4}$×$\frac{5}{4}$,
∴($\frac{5}{4}$)3=($\frac{4}{5}$)-3;
(3)由(1)、(2)知,($\frac{b}{a}$)-m=($\frac{a}{b}$)m,
故答案为:=;
(4)原式=($\frac{1}{2}$×$\frac{3}{4}$)-4×($\frac{3}{4}$)4
=($\frac{1}{2}$)-4×($\frac{3}{4}$)-4×($\frac{3}{4}$)4
=$\frac{1}{(\frac{1}{2})^{4}}$×($\frac{3}{4}$)-4+4
=16×1
=16.
点评 本题主要考查有理数的乘方、负整数指数幂及幂的运算,熟练掌握有理数的乘方法则和幂的运算法则是解题的关键.


 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:初中数学 来源: 题型:填空题
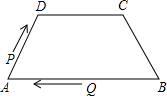 如图,在四边形ABCD中,AB∥DC,AD=BC=5,DC=7,AB=13,点P从点A出发,以3个单位/s的速度沿AD→DC向终点C运动,同时点Q从点B出发,以1个单位/s的速度沿BA向终点A运动,在运动期间,当四边形PQBC为平行四边形时,运动时间为3秒.
如图,在四边形ABCD中,AB∥DC,AD=BC=5,DC=7,AB=13,点P从点A出发,以3个单位/s的速度沿AD→DC向终点C运动,同时点Q从点B出发,以1个单位/s的速度沿BA向终点A运动,在运动期间,当四边形PQBC为平行四边形时,运动时间为3秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com