
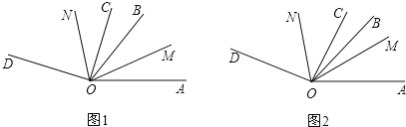
【题目】已知![]() ,
,![]() 、
、![]() 、
、![]() 、
、![]() 是
是![]() 内的射线.
内的射线.
(1)如图1,当![]() ,若
,若![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,求
,求![]() 的大小;
的大小;
(2)如图2,若![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,
,![]() ,
,![]() ,求
,求![]() .
.
【答案】(1)80°;(2)140°
【解析】
(1)根据角平分线的定义得∠BOM=![]() ∠AOB,∠BON=
∠AOB,∠BON=![]() ∠BOD,再根据角的和差得∠AOD=∠AOB+∠BOD,∠MON=∠BOM+∠BON,结合三式求解;(2)根据角平分线的定义∠MOC=
∠BOD,再根据角的和差得∠AOD=∠AOB+∠BOD,∠MON=∠BOM+∠BON,结合三式求解;(2)根据角平分线的定义∠MOC=![]() ∠AOC,∠BON=
∠AOC,∠BON=![]() ∠BOD,再根据角的和差得∠AOD=∠AOC+∠BOD-∠BOC,∠MON=∠MOC+∠BON-∠BOC结合三式求解.
∠BOD,再根据角的和差得∠AOD=∠AOC+∠BOD-∠BOC,∠MON=∠MOC+∠BON-∠BOC结合三式求解.
解:(1)∵OM平分∠AOB,ON平分∠BOD,
∴∠BOM=![]() ∠AOB,∠BON=
∠AOB,∠BON=![]() ∠BOD,
∠BOD,
∴∠MON=∠BOM+∠BON=![]() ∠AOB+
∠AOB+![]() ∠BOD=
∠BOD=![]() (∠AOB+∠BOD).
(∠AOB+∠BOD).
∵∠AOD=∠AOB+∠BOD=α=160°,
∴∠MON=![]() ×160°=80°;
×160°=80°;
(2)∵OM平分∠AOC,ON平分∠BOD,
∴∠MOC=![]() ∠AOC,∠BON=
∠AOC,∠BON=![]() ∠BOD,
∠BOD,
∵∠MON=∠MOC+∠BON-∠BOC,
∴∠MON=![]() ∠AOC+
∠AOC+![]() ∠BOD -∠BOC=
∠BOD -∠BOC=![]() (∠AOC+∠BOD )-∠BOC.
(∠AOC+∠BOD )-∠BOC.
∵∠AOD=∠AOB+∠BOD,∠AOC=∠AOB+∠BOC,
∴∠MON=![]() (∠AOB+∠BOC+∠BOD )-∠BOC=
(∠AOB+∠BOC+∠BOD )-∠BOC=![]() (∠AOD+∠BOC )-∠BOC,
(∠AOD+∠BOC )-∠BOC,
∵∠AOD=α,∠MON=60°,∠BOC=20°,
∴60°=![]() (α+20°)-20°,
(α+20°)-20°,
∴α=140°.


科目:初中数学 来源: 题型:
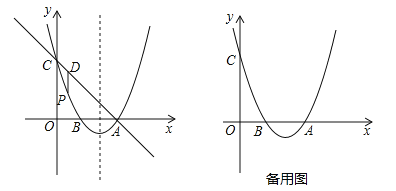
【题目】已知如图,抛物线y=x2+bx+c过点A(3,0),B(1,0),交y轴于点C,点P是该抛物线上一动点,点P从C点沿抛物线向A点运动(点P不与点A重合),过点P作PD∥y轴交直线AC于点D.
(1)求抛物线的解析式;
(2)求点P在运动的过程中线段PD长度的最大值;
(3)△APD能否构成直角三角形?若能请直接写出点P坐标,若不能请说明理由;
(4)在抛物线对称轴上是否存在点M使|MA﹣MC|最大?若存在请求出点M的坐标,若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
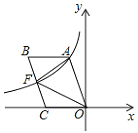
【题目】如图,四边形OABC是平行四边形,边OC在x轴的负半轴上,反比例函数![]() 的图象经过点A与BC的中点F,连接AF,OF,若△AOF的面积为12,则k的值为_______.
的图象经过点A与BC的中点F,连接AF,OF,若△AOF的面积为12,则k的值为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】目前“微信”、“支付宝”、“共享单车”和“网购”给我们的生活带来了很多便利,初二数学小组在校内对“你最认可的四大新生事物”进行调查,随机调查了![]() 人(每名学生必选一种且只能从这四种中选择一种)并将调查结果绘制成如下不完整的统计图.
人(每名学生必选一种且只能从这四种中选择一种)并将调查结果绘制成如下不完整的统计图.
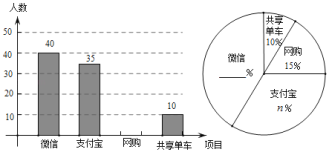
(1)根据图中信息求出![]() ,
,![]() ;
;
(2)请你帮助他们将这两个统计图补全;
(3)根据抽样调查的结果,请估算全校2000名学生中,大约有多少人最认可“微信”这一新生事物?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种商品的标价为500元/件,经过两次降价后的价格为320元/件,并且两次降价的百分率相同.
(1)求该种商品每次降价的百分率;
(2)若该商品进价为280元/件,两次降价共售此种商品100件,为使两次降价销售的总利润不少于8000元,则第一次降价后至少要售出这种商品多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在四边形ABCD中,AD//BC,对角线AC、BD交于点O,且AC=BD,下列四个命题中真命题是( )
A. 若AB=CD,则四边形ABCD一定是等腰梯形;
B. 若∠DBC=∠ACB,则四边形ABCD一定是等腰梯形;
C. 若![]() ,则四边形ABCD一定是矩形;
,则四边形ABCD一定是矩形;
D. 若AC⊥BD且AO=OD,则四边形ABCD一定是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ABCD中,已知AB=6,BE平分∠ABC交AD边于点E,点E将AD分为1:3两部分,则AD的长为( )
A. 8或24B. 8C. 24D. 9或24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某片果园有果树80棵,现准备多种一些果树提高果园产量,但是如果多种树,那么树之间的距离和每棵树所受光照就会减少,单棵树的产量随之降低,若该果园每棵果树产果y千克,增种果树x棵,它们之间的函数关系如图所示.

(1)求y与x之间的函数解析式;
(2)在投入成本最低的情况下,增种果树多少棵时,果园可以收获果实6750千克?
(3)当增种果树多少棵时,果园的总产量w(千克)最大?最大产量是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com