现有长度分别为2、4、6、7、8的五条线段,从中任取三条能构成三角形的概率为________.

分析:根据三角形的基本性质,任取三条共有10种可能,能构成三角形的有:267、278、467、468、678、478,则可求出概率.
解答:由题意知:任取三条共有10种可能,
而能构成三角形的有:267、278、467、468、678、478这6种可能,
所以从中任取三条能构成三角形的概率为
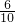
=

.
点评:根据随机事件概率大小的求法,找准两点:
①符合条件的情况数目;
②全部情况的总数.
二者的比值就是其发生的概率的大小.构成三角形的基本要求为两小边之和大于最大边.
