
【题目】如图,点A在反比例函数y=﹣ ![]() (x<0)的图象上移动,连接OA,作OB⊥OA,并满足∠OAB=30°.在点A的移动过程中,追踪点B形成的图象所对应的函数表达式为( )
(x<0)的图象上移动,连接OA,作OB⊥OA,并满足∠OAB=30°.在点A的移动过程中,追踪点B形成的图象所对应的函数表达式为( ) 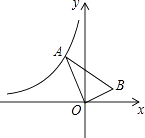
A.y= ![]() (x>0)
(x>0)
B.y= ![]() (x>0)
(x>0)
C.y= ![]() (x>0)
(x>0)
D.y= ![]() (x>0)
(x>0)
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠DAC是△ABC的一个外角. 实验与操作:
根据要求进行尺规作图,并在图中标明相应字母(保留作图痕迹,不写作法)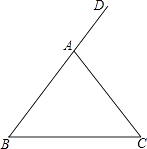
(1)作∠DAC的平分线AM;
(2)作线段AC的垂直平分线,与AM交于点F,与BC边交于点E,连接AE,CF.猜想并证明: 判断四边形AECF的形状并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读,后解答:
(1)由根式的性质计算下列式子得:
①![]() =3,②
=3,②![]() ,③
,③![]() ,④
,④![]() =5,⑤
=5,⑤![]() =0.
=0.
由上述计算,请写出![]() 的结果(a为任意实数).
的结果(a为任意实数).
(2)利用(1)中的结论,计算下列问题的结果:
①![]() ;
;
②化简:![]() (x<2).
(x<2).
(3)应用:
若![]() =3,求x的取值范围.
=3,求x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五一节,小丽独自一人去老家玩,家住在车站附近的姑姑到车站去接小丽.因为担心小丽下车后找不到路,姑姑一路小跑来到车站,结果客车晚点,休息一阵后,姑姑接到小丽,和小丽一起慢慢的走回了家.下列图象中,能反映以上过程中小丽姑姑离家的距离s与时间t的关系的大致图象是( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果三角形有一边上的中线长恰好等于这边的长,那么称这个三角形为“好玩三角形”.
(1)请用直尺和圆规画一个“好玩三角形”;
(2)如图在Rt△ABC中,∠C=90°,tanA= ![]() ,求证:△ABC是“好玩三角形”;
,求证:△ABC是“好玩三角形”;
(3)如图2,已知菱形ABCD的边长为a,∠ABC=2β,点P,Q从点A同时出发,以相同速度分别沿折线AB﹣BC和AD﹣DC向终点C运动,记点P经过的路程为s.
①当β=45°时,若△APQ是“好玩三角形”,试求 ![]() 的值;
的值;
②当tanβ的取值在什么范围内,点P,Q在运动过程中,有且只有一个△APQ能成为“好玩三角形”.请直接写出tanβ的取值范围.
(4)(本小题为选做题)
依据(3)的条件,提出一个关于“在点P,Q的运动过程中,tanβ的取值范围与△APQ是‘好玩三角形’的个数关系”的真命题(“好玩三角形”的个数限定不能为1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小敏在作⊙O的内接正五边形时,先做了如下几个步骤:
(i)作⊙O的两条互相垂直的直径,再作OA的垂直平分线交OA于点M,如图1;
(ii)以M为圆心,BM长为半径作圆弧,交CA于点D,连结BD,如图2.若⊙O的半径为1,则由以上作图得到的关于正五边形边长BD的等式是( )
A.BD2= ![]() OD
OD
B.BD2= ![]() OD
OD
C.BD2= ![]() OD
OD
D.BD2= ![]() OD
OD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校体育组为了了解学生喜欢的体育项目,从全校同学中随机抽取了若干名同学进行调查,每位同学从乒乓球、篮球、羽毛球、排球、跳绳中选择一项最喜欢的项目,并将调查的结果绘制成如下的两幅统计图.根据以上统计图,解答下列问题: 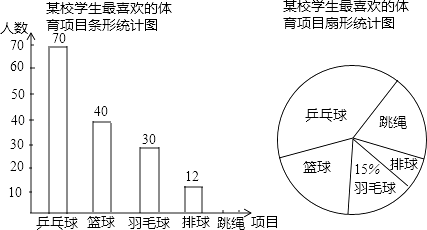
(1)这次被调查的共有多少名同学?并补全条形统计图.
(2)若全校有1200名同学,估计全校最喜欢篮球和排球的共有多少名同学?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列结论正确的是( )
A.x2﹣2是二次二项式
B.单项式﹣x2的系数是1
C.使式子 ![]() 有意义的x的取值范围是x>﹣2
有意义的x的取值范围是x>﹣2
D.若分式 ![]() 的值等于0,则a=±1
的值等于0,则a=±1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com