
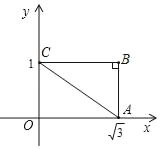
【题目】如图,在Rt△ABC中,∠B=90°,∠ACB=30°,其直角边分别与坐标轴垂直,已知顶点的坐标为A(![]() ,0),C(0,1).
,0),C(0,1).
(1)如果A关于BC对称的点是D,则点D的坐标为 ;
(2)过点B作直线m∥AC,交CD连线于E,求△BCE的面积.
科目:初中数学 来源: 题型:
【题目】如图,已知点E、F在直线AB上,点G在线段CD上,ED与FG交于点H,∠C=∠EFG,∠CED=∠GHD.
(1)求证:CE∥GF;
(2)试判断∠AED与∠D之间的数量关系,并说明理由;
(3)若∠EHF=80°,∠D=30°,求∠AEM的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
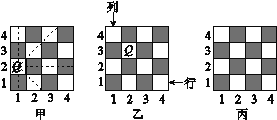
【题目】国际象棋、中国象棋和围棋号称世界三大棋种.国际象棋中的“皇后”的威力可比中国象棋中的“车”的威力大得多,“皇后”不仅能控制她所在的行与列中的每一个小方格,而且还能控制斜方向的两条直线上的每一个小方格.如图,甲是一个4×4的小方格棋盘,图中的“皇后Q”能控制图中虚线所经过的每一个小方格.
(1)在如图乙的小方格棋盘中有一“皇后Q”,她所在的位置可用(2,3)来表示,请说明“皇后Q”所在的位置是第几列第几行,并用这种表示方法分别写出该棋盘中不能被该“皇后Q”控制的四个位置;
(2)如图丙也是一个4×4的小方格棋盘,请在这个棋盘中放入四个“皇后Q”,使这四个“皇后Q”之间互不受对方控制(在图丙中的某四个小方格中标出字母Q即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
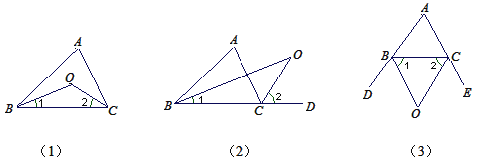
【题目】如图(1)所示,△ABC中,∠ABC,∠ACB的平分线交于点O,求证:∠BOC=90+![]() ∠A.
∠A.
变式1:如图(2)所示,∠ABC,∠ACD的平分线交于点O,求证:∠BOC=![]() ∠A.
∠A.
变式2:如图(3)所示,∠CBD,∠BCE的平分线交于点O,求证:∠BOC=90-![]() ∠A.
∠A.
查看答案和解析>>
科目:初中数学 来源: 题型:
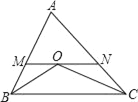
【题目】如图,在△ABC中,BO、CO分别平分∠ABC、∠ACB相交于点O,线段MN过点O与AB、AC分别交于M、N两点,且MN∥BC,若△AMN的周长等于12,则AB+AC的长等于_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知直线y= ![]() x+2与x轴交于点A,与y轴交于点C,抛物线y=ax2+4ax+b经过A.C两点,且与x轴交于另一点B.
x+2与x轴交于点A,与y轴交于点C,抛物线y=ax2+4ax+b经过A.C两点,且与x轴交于另一点B.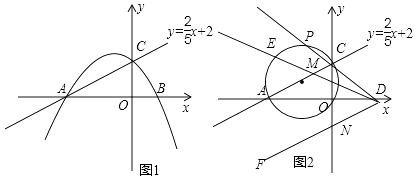
(1)求抛物线的解析式;
(2)若点Q在抛物线上,且△AQC与△BQC面积相等,求点Q的坐标;
(3)如图2,P为△AOC外接圆上弧ACO的中点,直线PC交x轴于点D,∠EDF=∠ACO,当∠EDF绕点D旋转时,DE交直线AC于点M,DF交y轴负半轴于点N.请你探究:CN﹣CM的值是否发生变化?若不变,求出其值;若变化,求出变化范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,点D,E分别是边AB,AC的中点,延长DE至点F,使EF=DE,则四边形ADCF一定是( ) 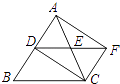
A.矩形
B.菱形
C.正方形
D.梯形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个多位自然数的任意两个相邻数位上,右边数位上的数总比左边数位上数大1,那么我们把这样的自然数叫做“相连数”.例如:234,4567,56789,…都是“相连数”.
(1)请直接写出最大的两位“相连数”与最小的三位“相连数”,并求它们的差.
(2)若某个“相连数”恰好等于其个位数的469倍,求这个“相连数”.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校九年级学生举行朗诵比赛,全年级学生都参加,学校对表现优异的学生进行表彰,设置一、二、三等奖各进步奖共四个奖项,赛后将九年级(1)班的获奖情况绘制成如图所示的两幅不完整的统计图,请根据图中的信息,解答下列问题: 
(1)九年级(1)班共有名学生;
(2)将条形图补充完整:在扇形统计图中,“二等奖”对应的扇形的圆心角度数是;
(3)如果该九年级共有1250名学生,请估计荣获一、二、三等奖的学生共有多少名.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com