
【题目】在一条东西走向河的一侧有一村庄C,河边原有两个取水点A,B,其中AB=AC,由于某种原因,由C到A的路现在已经不通,某村为方便村民取水决定在河边新建一个取水点H(A、H、B在一条直线上),并新修一条路CH,测得CB=3千米,CH=2.4千米,HB=1.8千米.
(1)问CH是否为从村庄C到河边的最近路?(即问:CH与AB是否垂直?)请通过计算加以说明;
(2)求原来的路线AC的长.

科目:初中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,AB//CD,AD⊥AB,∠B=60°,AB=10,BC=4,点P沿线段AB从点A向点B运动,设AP=x,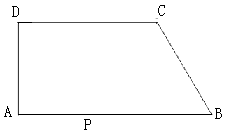
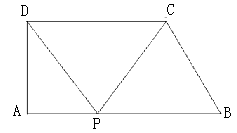
(1)求AD的长;
(2)点P在运动过程中,是否存在以A、P、D为顶点的三角形与以P、C、B为顶点的三角形相似?若存在,求出x的值;若不存在,请说明理由;
(3)直接写出:当△CDP为等腰三角形时x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若a、b、c是正数,下列各式,从左到右的变形不能用如图验证的是( )
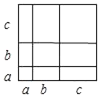
A. (b+c)2=b2+2bc+c2
B. a(b+c)=ab+ac
C. (a+b+c)2=a2+b2+c2+2ab+2bc+2ac
D. a2+2ab=a(a+2b)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年元旦期间,某超市打出促销广告,如下表所示:
一次性所购物品的原价 | 优惠办法 |
不超过200元 | 没有优惠 |
超过200元,但不超过600元 | 全部按九折优惠 |
超过600元 | 其中600元仍按九折优惠,超过600元部分按8折优惠 |
(1)小张一次性购买物品的原价为400元,则实际付款为 元;
(2)小王购物时一次性付款580元,则所购物品的原价是多少元?
(3)小赵和小李分别前往该超市购物,两人各自所购物品的原价之和为1200元,且小李所购物品的原价高于小赵,两人实际付款共1074元,则小赵和小李各自所购物品的原价分别是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲骑自行车从A地出发前往B地,同时乙步行从B地出发前往A地,如图的折线OPQ和线段EF,分表表示甲、乙两人与A地的距离![]() 、
、![]() 与他们所行时间
与他们所行时间![]() 之间的函数关系,且OP与EF相交于点M.
之间的函数关系,且OP与EF相交于点M.
![]() 求线段OP对应的
求线段OP对应的![]() 与x的函数关系式;
与x的函数关系式;
![]() 求
求![]() 与x的函数关系式以及A,B两地之间的距离;
与x的函数关系式以及A,B两地之间的距离;
![]() 求经过多少小时,甲、乙两人相距3km.
求经过多少小时,甲、乙两人相距3km.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD∥AB,OE平分∠AOD,OF⊥OE,OG⊥CD,∠CDO=50°,则下列结论:
① ∠AOE=65°;② OF平分∠BOD;③ ∠GOE=∠DOF;④ ∠AOE=∠GOD,其中正确结论的个数是( )

A. 4个B. 3个C. 2个D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l:y=﹣3x+3与x轴、y轴分别相交于A、B两点,抛物线y=ax2-2ax+a+4(a<0)经过点B.
(1)求该抛物线的函数表达式;
(2)已知点M是抛物线上的一个动点,并且点M在第一象限内,连接AM、BM,设点M的横坐标为m,△ABM的面积为S,求S与m的函数表达式,并求出S的最大值;
(3)在(2)的条件下,当S取得最大值时,动点M相应的位置记为点M′.
①写出点M′的坐标;
②将直线l绕点A按顺时针方向旋转得到直线l′,当直线l′与直线AM′重合时停止旋转,在旋转过程中,直线l′与线段BM′交于点C,设⊙B, ⊙M′都与直线l′相切,半径分别为R1、R2 , 当R1+R2最大时,求直线l′旋转的角度(即∠BAC的度数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题,如图,正方形ABCD。
(1)请在图①中作两条直线,使它们将正方形ABCD的面积三等分;
(2)如图②,在矩形ABCD中,AB=6,BC=9,在图②中过顶点A作两条直线,使它们将矩形ABCD的面积三等分,井说明理由;
(3)如图③,农博园有一块不规则的五边形ABCDE空地,其中AB∥CD、AE∥BC,AB=AC=100米,AE=160米,BC=120米,CD=62.5米,根据视觉效果和花期特点,农博园设计部门想在这片空地种上等面积的三种不同的花,要求从入口A点处修两条笔直的小路(小路的面积忽略不计)方便游客赏花,两条小路将这块地面积三等分.请通过计算画图说明其设计部们能否实现,若能实现请确定小路尽头的位置.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com