
【题目】小明购买了一套安居型商品房,他准备将地面铺上地砖,地面结构如图所示.请根据图中的数据(单位:m),解答下列问题:
(1)用含x、y的代数式表示地面总面积;
(2)若x=5,y=![]() ,铺1m2地砖的平均费用为80元,那么铺地砖的总费用为多少元?
,铺1m2地砖的平均费用为80元,那么铺地砖的总费用为多少元?

科目:初中数学 来源: 题型:
【题目】用同样大小的两种不同颜色的正方形纸片,按下图方式拼正方形.
第(1)个图形中有1个正方形;
第(2)个图形有1+3=4个小正方形;
第(3)个图形有1+3+5=9个小正方形
第(5)个图形有 个小正方形(直接写出结果);

(1)根据上面的发现我们可以猜想:1+3+5+7+…+(2n﹣1)= (用含n的代数式表示);
(2)请根据你的发现计算:①1+3+5+7+…+99= ;②101+103+105+…+199= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABD中,∠ABC和∠ACB的平分线交于点E,过点E作MN∥AB交AB于N,交AC于N,若BM+CN=8,则线段MN的长为( )
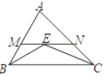
A. 5B. 6C. 7D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)看一看下面两组式子:(3×5)2 与 32×52,[(- ![]() )×4]2 与(-
)×4]2 与(- ![]() )2×42;每组的两个算式的计算结果是否相等?
)2×42;每组的两个算式的计算结果是否相等?
(2)想一想(ab)2等于什么?猜一猜,当 n 为正整数时,(ab)n 等于什么?你能用一句 话叙述你的所得到的结果吗?
(3)运用上述结论计算下列各题
①(-8)2019×(![]() )2019
)2019
②(-1![]() )2020×(
)2020×(![]() )2020
)2020
查看答案和解析>>
科目:初中数学 来源: 题型:
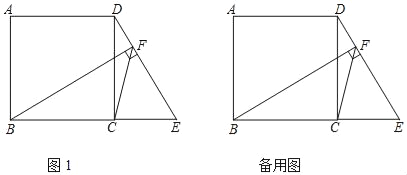
【题目】如图1,正方形ABCD中,点E是BC延长线上一点,连接DE,过点B作BF⊥DE于点F,连接FC
.
(1)求证:∠FBC=∠CDF.
(2)作点C关于直线DE的对称点G,连接CG,FG.
①依据题意补全图形;
②用等式表示线段DF,BF,CG之间的数量关系并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴是学习有理数的一种重要工具,任何有理数都可以用数轴上的点表示,这样能够运用数形结合的方法解决一些问题.
如图,将一条数轴在原点O和点B处各折一下,得到一条“折线数轴”.图中点A表示-10,点B表示10,点C表示18,我们称点A和点C在数轴上相距28个长度单位.动点P从点A出发,以2单位秒的速度沿着折线数抽”的正方向运动,从点O运动到点B期间速度变为原来的一半,之后立刻恢复原速;同时,动点Q从点C出发,以1单位秒的速度沿着数轴的负方向运动,从点B运动到点O期间速度变为原来的两倍,之后也立刻恢复原速.当点P到达点C时,两点都停上远动.设运动的时间为1秒.问:
(1)t=2秒时,点P在“折线数轴”上所对应的数是_______;点P到点Q的距离是_____单位长度;
(2)动点P从点4运动至C点需要_______秒;
(3)P、Q两点相遇时,求出t的值和此时相遇点M在“折线数轴”上所对应的数;
(4)如果动点P、O两点在数轴上相距的长度与Q、B两点在数轴上相距的长度相等,直接写出t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B 两乡分别由大米 200 吨、300 吨.现将这些大米运至 C、D 两个粮站储存.已知 C 粮站可 储存 240 吨,D 粮站可储存 200 吨,从 A 乡运往 C、D 两处的费用分别为每吨 20 元和 25 元,B 乡 运往 C、D 两处的费用分别为每吨 15 元和 18 元.设 A 乡运往 C 粮站大米 x 吨.A、B 两乡运往两 个粮站的运费分别为 yA、yB 元.
(1)请填写下表,并求出 yA、yB 与 x 的关系式:
C 站 | D 站 | 总计 | |
A 乡 | x 吨 | 200 吨 | |
B 乡 | 300 吨 | ||
总计 | 240 吨 | 260 吨 | 500 吨 |
(2)试讨论 A、B 乡中,哪一个的运费较少;
(3)若 B 乡比较困难,最多只能承受 4830 元费用,这种情况下,运输方案如何确定才能使总运费 最少?最少的费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】暑假期间,小明和父母一起开车到距家200千米的景点旅游.出发前,汽车油箱内储油45升,当行驶150千米时,发现油箱剩余油量为30升.(假设行驶过程中汽车的耗油量是均匀的.)
(1)写出用行驶路程x(千米)来表示剩余油量Q(升)的代数式;
(2)当x=300千米时,求剩余油量Q的值;
(3)当油箱中剩余油量少于3升时,汽车将自动报警.如果往返途中不加油,他们能否在汽车报警前回到家?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1,抛物线与x轴交于A(﹣1,0),B(3,0),顶点为D(1,﹣4),点P为y轴上一动点.
(1)求抛物线的解析式;
(2)在y轴的负半轴上是否存在点P,使△BDP是等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.
(3)如图2,点![]() 在抛物线上,求
在抛物线上,求![]() 的最小值.
的最小值.
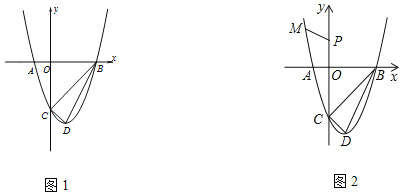
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com