
 如图,抛物线y=-x2+4x+5与x轴交于A、B两点,与y轴交于点C.已知M(0,1),E(a,0),F(a+1,0),点P是第一象限内的抛物线上的动点.△PCM是以CM为底的等腰三角形,则点P的坐标为(2+$\sqrt{6}$,3);当a=$\frac{\sqrt{6}+1}{4}$时,四边形PMEF周长最小.
如图,抛物线y=-x2+4x+5与x轴交于A、B两点,与y轴交于点C.已知M(0,1),E(a,0),F(a+1,0),点P是第一象限内的抛物线上的动点.△PCM是以CM为底的等腰三角形,则点P的坐标为(2+$\sqrt{6}$,3);当a=$\frac{\sqrt{6}+1}{4}$时,四边形PMEF周长最小. 分析 根据抛物线的解析式易求点C的坐标,再根据四边形PMEF的四条边中,PM、EF长度固定,因此只要ME+PF最小,则PMEF的周长将取得最小值.如答图3所示,将点M向右平移1个单位长度(EF的长度),得M1(1,1);作点M1关于x轴的对称点M2,则M2(1,-1);连接PM2,与x轴交于F点,此时ME+PF=PM2最小.
解答 解:∵y=-x2+4x+5与y轴交于点C,
∴点C的坐标为(0,5)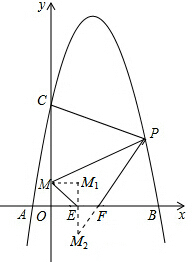
又∵M(0,1),△PCM是以点P为顶点的等腰三角形,
∴点P的纵坐标为3.
令y=-x2+4x+5=3,解得x=2±$\sqrt{6}$.
∵点P在第一象限,∴P(2+$\sqrt{6}$,3).
四边形PMEF的四条边中,PM、EF长度固定,因此只要ME+PF最小,则PMEF的周长将取得最小值.(如图所示)
将点M向右平移1个单位长度(EF的长度),得M1(1,1);
作点M1关于x轴的对称点M2,则M2(1,-1);
连接PM2,与x轴交于F点,此时ME+PF=PM2最小.
设直线PM2的解析式为y=mx+n,将P(2+$\sqrt{6}$,3),M2(1,-1)代入得:
$\left\{\begin{array}{l}{(2+\sqrt{6})m+n=3}\\{m+n=-1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=\frac{4\sqrt{6}-4}{5}}\\{n=\frac{-4\sqrt{6}-1}{5}}\end{array}\right.$
∴y=$\frac{4\sqrt{6}-4}{5}$x-$\frac{4\sqrt{6}+1}{5}$.
当y=0时,解得x=$\frac{\sqrt{6}+5}{4}$.∴F($\frac{\sqrt{6}+5}{4}$,0).
∵a+1=,∴a=$\frac{\sqrt{6}+1}{4}$.
∴a=$\frac{\sqrt{6}+1}{4}$时,四边形PMEF周长最小.
故答案为:(2+$\sqrt{6}$,3),$\frac{\sqrt{6}+1}{4}$.
点评 本题是二次函数综合题,用到的知识点等腰三角形的判定和性质、二元一次方程组的运用以及二次函数的最值和轴对称-最短路线的性质.试题计算量偏大,注意认真计算.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 市政府决定对市直机关500户家庭的用水情况作一次调查,调查小组随机抽查了其中的100户家庭一年的月平均用水量(单位:吨),并将调查结果制成了如图所示的条形统计图.
市政府决定对市直机关500户家庭的用水情况作一次调查,调查小组随机抽查了其中的100户家庭一年的月平均用水量(单位:吨),并将调查结果制成了如图所示的条形统计图.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m>-$\frac{1}{2}$ | B. | m<3 | C. | -$\frac{1}{2}$<m<3 | D. | -$\frac{1}{2}$<m≤3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com