
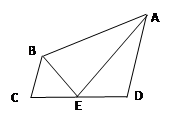
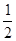 S四边形ABCD
S四边形ABCD| A.1 | B.2 | C.3 | D.4 |
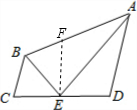
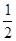 ∠DEF+
∠DEF+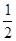 ∠CEF=
∠CEF=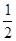 ×180°=90°;
×180°=90°;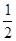 S四边形BCEF+
S四边形BCEF+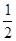 S四边形EFAD=
S四边形EFAD=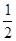 S四边形ABCD.
S四边形ABCD.

 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源:不详 题型:单选题
| A.各角都相等的多边形是正多边形. |
| B.有一组对边平行的四边形是梯形. |
| C.对角线互相垂直的四边形是菱形. |
| D.有一边上的中线等于这边一半的三角形是直角三角形. |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 中,
中, 为锐角,点
为锐角,点 为射线
为射线 上一点,联结
上一点,联结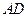 ,以
,以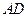 为一边且在
为一边且在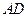 的右侧作正方形
的右侧作正方形 .
. ,
, ,
, 在线段
在线段 上时(与点
上时(与点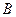 不重合),如图2,线段
不重合),如图2,线段 所在直线的位置关系为 __________ ,线段
所在直线的位置关系为 __________ ,线段 的数量关系为 ;
的数量关系为 ; 在线段
在线段 的延长线上时,如图3,①中的结论是否仍然成立,并说明理由;
的延长线上时,如图3,①中的结论是否仍然成立,并说明理由; | |||||
 | |||||
 | |||||
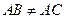 ,
, 是锐角,点
是锐角,点 在线段
在线段 上,当
上,当 满足什么条件时,
满足什么条件时, (点
(点 不重合),并说明理由.
不重合),并说明理由. 查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 C于点E,过点E作DH的垂线交线段AB、CD于点F、G.
C于点E,过点E作DH的垂线交线段AB、CD于点F、G. 明理由.
明理由.

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com