
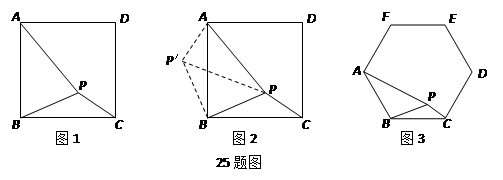
【问题】如图17-1,在正方形ABCD内有一点P,PA= ,PB=
,PB=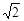 ,PC=1,求∠BPC的度数.
,PC=1,求∠BPC的度数.
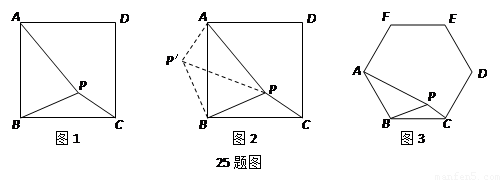
分析根据已知条件比较分散的特点,我们可以通过旋转变换将分散的已知条件集中在一起,于是将△BPC绕点B逆时针旋转90°,得到了△BP′A(如图17-2),然后连结PP′.
解决问题请你通过计算求出图17-2中∠BPC的度数;
类比研究 如图17-3,若在正六边形ABCDEF内有一点P,且PA=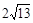 ,PB=4,PC=2.
,PB=4,PC=2.
(1)∠BPC的度数为 ; (2)直接写出正六边形ABCDEF的边长为 .
解:【解决问题】
根据【分析】中的思路,得到如图6所示的图形,

根据旋转的性质可得PB=P′B, PC=P′A,
又因为BC=AB, ∴△PBC≌△P′BA,
∴∠PBC=∠P′BA ,∠BPC=∠BP′A , PB= P′B= ,
,
∴∠P′BP=90°,所以△P′BP为等腰直角三角形,
则有P′P=2,∠BP′P=45°. ……………………2分
又因为PC=P′A=1,P′P =2,PA= ,
,
满足P′A2+ P′P2= PA2,由勾股定理的逆定理可知∠AP′P=90°, ……………4分
因此∠BPC=∠BP′A=45°+90°=135°. ……………………6分
【类比研究】(1)120°; ……………………8分
(2) .
……………………10分
.
……………………10分
参考提示:
(1)仿照【分析】中的思路,将△BPC绕点B逆时针旋转120°,得到了△BP′A,然后连结PP′.如图7所示,根据旋转的性质可得:△PBC≌△P′BA,

△BPP′为等腰三角形,PB= P′B=4,PC=P′A=2,∠BPC=∠BP′A,
∵∠ABC=120°,∴∠PBP′=120°,∠BP′P=30°,
∴求得PP′= ,
,
在△APP′中,∵PA= ,PP′=
,PP′= ,P′A=2,
,P′A=2,
满足P′A2+ P′P2= PA2,所以∠AP′P=90°.
∠BPC=∠BP′A=30°+90°=120°.
(2)延长A P′ 做BG⊥AP′于点G,如图8所示,

在Rt△P′BG中,P′B=4,∠BP′G=60°,
所以P′G=2,BG= ,则AG= P′G +P′A =2+2=4,
,则AG= P′G +P′A =2+2=4,
故在Rt△ABG中,根据勾股定理得AB= .
.
【解析】将△BPC绕点B逆时针旋转120°,得到了△BP′A,然后连结PP′.如图7所示,根据旋转的性质可得:△PBC≌△P′BA,后根据勾股定理得出∠AP′P=90°,从而得出∠BPC=120°;延长A P′ 做BG⊥AP′,构建直角三角形,也是由勾股定理得出AB= 。
。


科目:初中数学 来源: 题型:
【问题】如图17-1,在正方形ABCD内有一点P,PA=![]() ,PB=
,PB=![]() ,PC=1,求∠BPC的度数.
,PC=1,求∠BPC的度数.
分析根据已知条件比较分散的特点,我们可以通过旋转变换将分散的已知条件集中在一起,于是将△BPC绕点B逆时针旋转90°,得到了△BP′A(如图17-2),然后连结PP′.
解决问题请你通过计算求出图17-2中∠BPC的度数;
类比研究 如图17-3,若在正六边形ABCDEF内有一点P,且PA=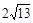 ,PB=4,PC=2.
,PB=4,PC=2.
(1)∠BPC的度数为 ; (2)直接写出正六边形ABCDEF的边长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
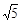 ,PB=
,PB=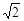 ,PC=1,求∠BPC的度数.
,PC=1,求∠BPC的度数.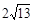 ,PB=4,PC=2.
,PB=4,PC=2.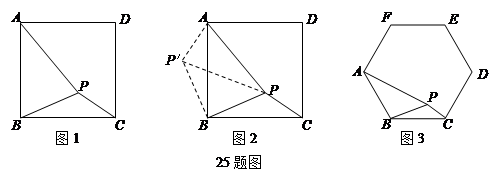
查看答案和解析>>
科目:初中数学 来源:2012-2013学年浙江省湖州十一中九年级第二学期期中考试数学试卷(带解析) 题型:解答题
【问题】如图,在正方形ABCD内有一点P,PA=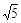 ,PB=
,PB=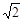 ,PC=1,求∠BPC的度数.
,PC=1,求∠BPC的度数.
分析根据已知条件比较分散的特点,我们可以通过旋转变换将分散的已知条件集中在一起,于是将△BPC绕点B逆时针旋转90°,得到了△BP′A(如图),然后连结PP′.
解决问题请你通过计算求出图17-2中∠BPC的度数;
【类比研究】如图,若在正六边形ABCDEF内有一点P,且PA= ,PB=4,PC=2.
,PB=4,PC=2.
(1)∠BPC的度数为 ;(2)直接写出正六边形ABCDEF的边长为 .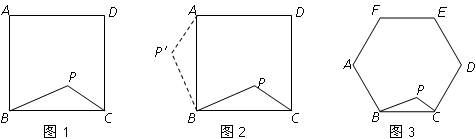
查看答案和解析>>
科目:初中数学 来源:2012届河北石家庄初中毕业班教学质量检测数学试卷(带解析) 题型:解答题
【问题】如图17-1,在正方形ABCD内有一点P,PA= ,PB=
,PB= ,PC=1,求∠BPC的度数.
,PC=1,求∠BPC的度数.
分析根据已知条件比较分散的特点,我们可以通过旋转变换将分散的已知条件集中在一起,于是将△BPC绕点B逆时针旋转90°,得到了△BP′A(如图17-2),然后连结PP′.
解决问题请你通过计算求出图17-2中∠BPC的度数;
类比研究如图17-3,若在正六边形ABCDEF内有一点P,且PA=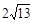 ,PB=4,PC=2.
,PB=4,PC=2.
(1)∠BPC的度数为 ;(2)直接写出正六边形ABCDEF的边长为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com