
【题目】如图,直线y=kx+b分别交x轴、y轴于A(1,0)、B(0,﹣1),交双曲线y=![]() 于点C、D.
于点C、D.
(1)求k、b的值;
(2)写出不等式kx+b>![]() 的解集.
的解集.

科目:初中数学 来源: 题型:
【题目】为了改善教室空气环境,某校九年级1班班委会计划到朝阳花卉基地购买绿植.已知该基地一盆绿萝与一盆吊兰的价格之和是12元.班委会决定用60元购买绿萝,用90元购买吊兰,所购绿萝数量正好是吊兰数量的两倍.
(1)分别求出每盆绿萝和每盆吊兰的价格;
(2)该校九年级所有班级准备一起到该基地购买绿萝和吊兰共计90盆,其中绿萝数量不超过吊兰数量的一半,该基地特地对吊兰价格给出了如下的优惠政策,一次性购买的吊兰超过20盆时,超过部分的吊兰每盆的价格打8折,根据该基地的优惠信息,九年级购买这两种绿植各多少盆时总费用最少?最少费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个正方体礼盒如图所示,六个面分别写有“祝”“福”“祖”“国”“万”“岁”,其中“祝”的对面是“祖”,“万”的对面是“岁”,则它的表面展开图可能是( )
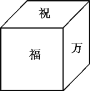
A. 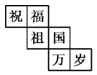 B.
B. 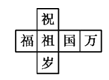 C.
C. 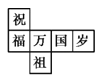 D.
D. 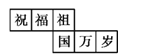
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一张正三角形纸片剪成四个小正三角形,得到4个小正三角形,称为第一次操作;然后,将其中的一个正三角形再剪成四个小正三角形,共得到7个小正三角形,称为第二次操作;再将其中的一个正三角形再剪成四个小正三角形,共得到10个小正三角形,称为第三次操作;…,根据以上操作,若要得到2014个小正三角形,则需要操作的次数是( )次.
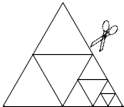
A.669B.670C.671D.672
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阳光集团新进了20台电视机和30台电饭煲,计划将这50台电器调配给下属的甲、乙两个商店销售,其中40台给甲商店,10台给乙商店.两个商店销售这两种电器每台的利润(元)如下表:
电视机 | 电饭煲 | |
甲商店/元 | 100 | 60 |
乙商店/元 | 80 | 50 |
(1)设集团调配给甲商店x台电视机,则调配给甲商店电饭煲 台,调配给乙商店电视机 台、电饭煲 台;
(2)求出x的取值范围;
(3)如果阳光集团卖出这50台电器想要获得的总利润为3650元,请求出x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店经销一种空气净化器,每台净化器的成本价为200元.经过一段时间的销售发现,每月的销售量y(台)与销售单价x(元)的关系为y=﹣2x+800.
(1)该商店每月的利润为W元,写出利润W与销售单价x的函数关系式;
(2)若要使每月的利润为20000元,销售单价应定为多少元?
(3)商店要求销售单价不低于280元,也不高于350元,求该商店每月的最高利润和最低利润分别为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(-2,2),B(8,12)在抛物线y=ax2+bx上.
(1)求抛物线的解析式;
(2)如图1,点F的坐标为(0,m)(m>4),直线AF交抛物线于另一点G,过点G作x轴的垂线,垂足为H,设抛物线与x轴的正半轴交于点E,连接FH、AE,求![]() 之值(用含m的代数式表示);
之值(用含m的代数式表示);
(3)如图2,直线AB分别交x轴、y轴于C、D两点,点P从点C出发,沿射线CD方向匀速运动,速度为每秒![]() 个单位长度,同时点Q从原点O出发,沿x轴正方向匀速运动,速度为每秒1个单位长度,点M是直线PQ与抛物线的一个交点,当运动到t秒时,QM=3PM,求t的值.
个单位长度,同时点Q从原点O出发,沿x轴正方向匀速运动,速度为每秒1个单位长度,点M是直线PQ与抛物线的一个交点,当运动到t秒时,QM=3PM,求t的值.
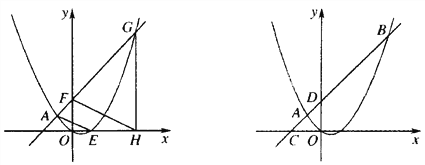
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△AEB和Rt△AFC中,∠E=∠F=90°,BE=CF.BE与AC相交于点M,与CF相交于点D,AB与CF相交于点N,∠EAC=∠FAB.有下列结论:①∠B=∠C;②CD=DN;③CM=BN;④△ACN≌△ABM.其中正确结论的序号是________.
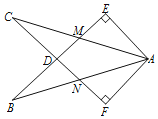
查看答案和解析>>
科目:初中数学 来源: 题型:
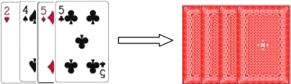
【题目】如图,甲、乙用这4张扑克牌玩游戏,他俩将扑克牌洗匀后背面朝上,放置在桌面上.
(1)甲从中任抽取一张,抽到4的概率是多少?
(2)甲、乙没人抽一张,甲先抽,乙后抽,抽出的牌不放回,甲、乙约定;只有甲抽到的牌面数字比乙大时甲胜.请你用树状图或列表法说明甲、乙获胜的机会是否相同.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com