
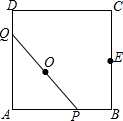
 如图,正方形ABCD的边长是4,E是BC的中点,动点P、Q在正方形ABCD的边上运动,且PQ=4.若点P从点A出发,沿A→B→E的线路,向点E运动,相应的,点Q在DA,AB上运动.则点P从A到E的运动过程中,PQ的中点O所经过的路线长等于$\frac{4π}{3}$.
如图,正方形ABCD的边长是4,E是BC的中点,动点P、Q在正方形ABCD的边上运动,且PQ=4.若点P从点A出发,沿A→B→E的线路,向点E运动,相应的,点Q在DA,AB上运动.则点P从A到E的运动过程中,PQ的中点O所经过的路线长等于$\frac{4π}{3}$.  同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:填空题
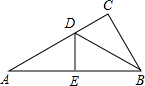 如图,在Rt△ABC中,∠C=90°,BD平分∠ABC,交AC于D,沿DE所在直线折叠,使点B恰好与点A重合,若CD=3,AB=8,则DB的值为5.
如图,在Rt△ABC中,∠C=90°,BD平分∠ABC,交AC于D,沿DE所在直线折叠,使点B恰好与点A重合,若CD=3,AB=8,则DB的值为5.查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 今年“五一”假期,某数学活动小组组织一次登山话动.他们从山脚下点A出发沿斜坡AB到达点B,再从点B沿斜坡BC到达山巅点C,路线如图所示. 斜坡AB的长为1 000米,斜坡BC的长为400米,在C点测得点B的俯角为30°.已知点A的海拔高度为121米,点C的海拔高度为921米.
今年“五一”假期,某数学活动小组组织一次登山话动.他们从山脚下点A出发沿斜坡AB到达点B,再从点B沿斜坡BC到达山巅点C,路线如图所示. 斜坡AB的长为1 000米,斜坡BC的长为400米,在C点测得点B的俯角为30°.已知点A的海拔高度为121米,点C的海拔高度为921米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,我们把杜甫(绝句)整齐排列放在平面直角坐标系中:
如图,我们把杜甫(绝句)整齐排列放在平面直角坐标系中:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 为迎接2014年世界杯足球赛,某商家购进甲、乙两种纪念品.甲种纪念品的进货价y甲(元/件)与进货数量x甲(件)的关系如图所示.
为迎接2014年世界杯足球赛,某商家购进甲、乙两种纪念品.甲种纪念品的进货价y甲(元/件)与进货数量x甲(件)的关系如图所示. 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com