
 的图象向上平移2个单位得反比例函数______的图象,若再向右平移2个单位后可以得到反比例函数______的图象;
的图象向上平移2个单位得反比例函数______的图象,若再向右平移2个单位后可以得到反比例函数______的图象; 的图象可以由函数
的图象可以由函数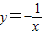 图象如何平移得到的;
图象如何平移得到的; 的图象将此函数向右平移2个单位后,再进行上下平移,使新函数的图象与坐标轴的两个交点与原点构成一个等腰三角形,求新函数的解析式.
的图象将此函数向右平移2个单位后,再进行上下平移,使新函数的图象与坐标轴的两个交点与原点构成一个等腰三角形,求新函数的解析式. 化为y=-
化为y=- +2的形式,再根据函数图象平移的法则进行解答即可;
+2的形式,再根据函数图象平移的法则进行解答即可; +b,再由坐标轴上点的坐标特点得出函数图象与两坐标轴的交点,由等腰三角形的性质即可求出b的值.
+b,再由坐标轴上点的坐标特点得出函数图象与两坐标轴的交点,由等腰三角形的性质即可求出b的值. 的图象向上平移2个单位后得到一个新的函数的图象的解析式为y=
的图象向上平移2个单位后得到一个新的函数的图象的解析式为y= +2;
+2; +2的图象向右平移2个单位后的图象的解析式为y=
+2的图象向右平移2个单位后的图象的解析式为y= +2.
+2. +2,y=
+2,y= +2;
+2; 可化为y=-
可化为y=- +2的形式,
+2的形式, 先向左平移1个单位,再向上平移2个单位即可得到函数y=
先向左平移1个单位,再向上平移2个单位即可得到函数y= 的图象;
的图象; +b,
+b, +b,令y=0,则x=
+b,令y=0,则x= ,
, +b)、(
+b)、( ,0),
,0), +b=±
+b=±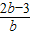 ,解得b=2,-2,
,解得b=2,-2, ,
, 时函数图象与坐标轴的交点只有一个是原点,故舍去,
时函数图象与坐标轴的交点只有一个是原点,故舍去, +2或y=
+2或y= -2.
-2.

科目:初中数学 来源: 题型:
|
|
|

|
|
查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
| x |
| 3 |
| x |
| 3 |
| x |
| 3 |
| x-2 |
| 3 |
| x-2 |
| 2x+1 |
| x+1 |
| 1 |
| x |
| 3 |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 的图象向上平移2个单位得反比例函数______的图象,若再向右平移2个单位后可以得到反比例函数______的图象;
的图象向上平移2个单位得反比例函数______的图象,若再向右平移2个单位后可以得到反比例函数______的图象; 的图象可以由函数
的图象可以由函数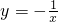 图象如何平移得到的;
图象如何平移得到的; 的图象将此函数向右平移2个单位后,再进行上下平移,使新函数的图象与坐标轴的两个交点与原点构成一个等腰三角形,求新函数的解析式.
的图象将此函数向右平移2个单位后,再进行上下平移,使新函数的图象与坐标轴的两个交点与原点构成一个等腰三角形,求新函数的解析式.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| 3 |
| x |
| 2x+1 |
| x+1 |
| 1 |
| x |
| 3 |
| x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com