
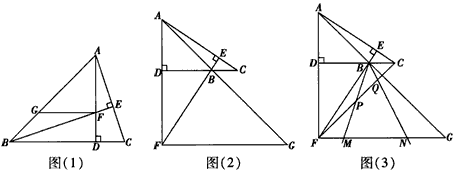
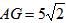 ,DC=3,将一个45°角的顶点与点B重合并绕点B旋转,这个角的两边分别交线段FG于M、N两点(如图(3)),连接CF,线段CF分别与线段BM、线段BN相交于P、Q两点,若
,DC=3,将一个45°角的顶点与点B重合并绕点B旋转,这个角的两边分别交线段FG于M、N两点(如图(3)),连接CF,线段CF分别与线段BM、线段BN相交于P、Q两点,若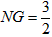 ,求线段PQ的长。
,求线段PQ的长。| 解:(1)证明:∵∠ADB=90°,∠ABC=45°, ∴∠BAD=∠ABC=45°, ∴AD=BD, ∵∠BEC=90°, ∴∠CBE+∠C=90°, ∵∠DAC+∠C=90°, ∴∠CBE=∠DAC, ∴△FDB≌△CDA ∵GF∥BD, ∴∠AGF=∠ABC=45°, ∴∠AGF=∠BAD, ∴FA=FG, ∴FG+DC=FA+DF=AD; |
|
| (2)FG-DC=AD; | |
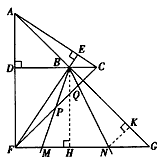
| (3)如图,∵∠ABC=135°, ∴∠ABD=45°, ∵∠ADB=90°, ∴∠DAB=∠DBA=45°, ∴AD=BD, ∵FG∥BC, ∴∠G=∠DBA=∠DAB, ∴AF=FG, FG2+AF2=AG2, ∴FG=AF=5, ∵DC=3,由(2)知:FG-DC=AD, ∴AD=BD=2, ∴BC=1,DF=3, ∴△FDC为等腰直角三角形, ∴ 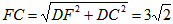 , ,分别过B、N作BH⊥FG于点H,NK⊥BC于点K, ∴四边形DFHB为矩形, ∴HF=BD=2,BH=DF=3,BH=HG=3, ∴ 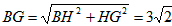 , ,∵sinG= 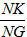 , ,∴ 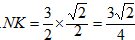 , ,又∵NK=KG, 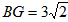 , ,∴BK=BG-KG=BC-NK= 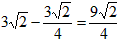 , ,∵∠MBN=∠HBG=45°, ∴∠MBH=∠NBK, ∵∠MHB=∠NKB=90°, ∴△MBH∽△NBK, ∴ 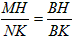 , ,∴MH=1, ∴FM=1, ∵BC∥FG, ∴∠BCF=∠CFN, ∵∠BPC=∠MPF,CB=FM, ∴△BPC≌△MPF, ∴ 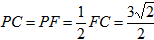 , ,∵∠BQC=∠NQF,∠BCF=∠CFN, ∴△BCQ∽△NFQ, ∴ 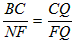 , ,∴ 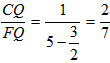 , ,∴ 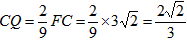 , ,∴ 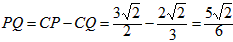 。 。 |
 |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
| 2 |
| 3 |
| 2 |
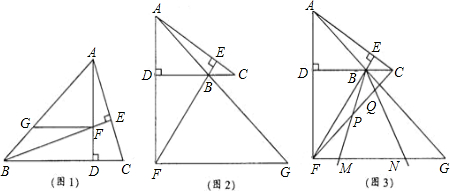
查看答案和解析>>
科目:初中数学 来源: 题型:
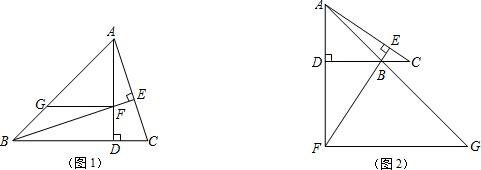
查看答案和解析>>
科目:初中数学 来源:2009年全国中考数学试题汇编《三角形》(12)(解析版) 题型:解答题
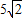 ,DC=3,将一个45°角的顶点与点B重合并绕点B旋转,这个角的两边分别交线段FG于M、N两点(如图3),连接CF,线段CF分别与线段BM、线段BN相交于P、Q两点,若NG=
,DC=3,将一个45°角的顶点与点B重合并绕点B旋转,这个角的两边分别交线段FG于M、N两点(如图3),连接CF,线段CF分别与线段BM、线段BN相交于P、Q两点,若NG= ,求线段PQ的长.
,求线段PQ的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com