
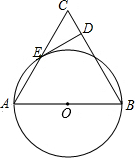
 在等边三角形△ABC中,以AB为直径的⊙O与AC交于点E,DE⊥BC于点D.
在等边三角形△ABC中,以AB为直径的⊙O与AC交于点E,DE⊥BC于点D.分析 (1)由等边三角形的性质可知∠A=∠C=60°,则可求得∠CED=30°,然后证明△AEO为等边三角形,则可得到∠AEO=60°,于是可求得∠DEO=90°;
(2)连结OE、过点O作OF⊥BC,垂足为F.依据含30°直角三角形的性质可得到CD=BF=$\frac{1}{2}$R(⊙O的半径),然后证明EOFD为矩形可得到DF=EO=R.
解答 解:(1)连结OE.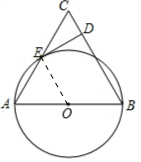
∵△ABC为等边三角形,
∴∠A=∠C=60°.
又∵OE=OA,
∴△AEO为等边三角形.
∴∠AEO=60°.
∵ED⊥BC,
∴∠EDC=90°.
∴∠CED=30°.
∴∠OED=90°.
∴ED是⊙O的切线.
(2)连结OE、过点O作OF⊥BC,垂足为F.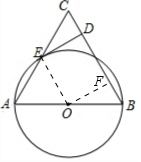
∵△ABC为等边三角形,AB=2R,△AEO为等边三角形,
∴EC=R.
∴CD=$\frac{1}{2}$EC=$\frac{1}{2}$R.
同理FB=$\frac{1}{2}$R.
∵DE⊥BC,OF⊥BC,
∴∠EDF=∠DFO=90°.
∵由(1)得∠OED=90°,
∴四边形EOFD为矩形.
∴DF=EO=R.
∴$\frac{DC}{BD}$=$\frac{\frac{1}{2}R}{R+\frac{1}{2}R}$=$\frac{1}{3}$.
点评 本题主要考查的是切线的判定、等边三角形的性质和判定、矩形的判定,掌握本题的辅助线的作法是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | (5,-1) | B. | (-1,-1) | C. | (-1,3) | D. | (5,3) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图是一块破损的矩形玻璃,只有一条边AB保存完好,现在为了再回收利用这块玻璃,需要在其内部裁出一个以AB为一边的最大矩形,请画出裁痕.(不写作法,保留作图痕迹)
如图是一块破损的矩形玻璃,只有一条边AB保存完好,现在为了再回收利用这块玻璃,需要在其内部裁出一个以AB为一边的最大矩形,请画出裁痕.(不写作法,保留作图痕迹)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 行驶时间t(h) | 0 | 1 | 2 | 3 | … |
| 剩余油量Q(L) | 42 | 36 | 30 | 24 | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com