Question

【题目】如图，直线y=x+2与抛物线y=ax2+bx+6（a≠0）相交于A（，）和B（4，m），点P是线段AB上异于A、B的动点，过点P作PC⊥x轴于点D，交抛物线于点C．当△PAC为直角三角形时点P的坐标 ．

Answer 1

【答案】（3，5）或（，）．

【解析】

试题分析：由于P点不可能为直角顶点，因此就只有两种情况：若A为直角顶点，过A作AB的垂线与抛物线的交点即为C点，过C作y轴的平行线与AB的交点即为P点；若C为直角顶点，过A作x轴的平行线与抛物线的另一个交点即为C点，过C作y轴的平行线与AB的交点即为P点．

解：∵直线y=x+2过点B（4，m），

∴m=6，

∴B（4，6）．

将A、B两点坐标代入抛物线解析式得：，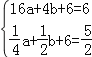

解得：

∴抛物线的解析式为：y=2x2﹣8x+6．

①若A为直角顶点，如图1，

设AC的解析式为：y=﹣x+b，

将A点代入y=﹣x+b得b=3

∴AC的解析式为y=﹣x+3，

由，解得：或（舍去）

令P点的横坐标为3，则纵坐标为5，

∴P（3，5）；

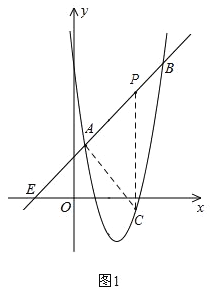
②若C为直角顶点，如图2，

令，解得：x=或x=（舍去），

令P点的横坐标为，则纵坐标为，

∴P（，）；

故答案为：（3，5）或（，）．