
【题目】如图1,直线m与直线n垂直相交于O,点A在直线m上运动,点B 在直线n上运动,AC、BC分别是∠BAO和∠ABO的角平分线.
(1)求∠ACB的大小;
(2)如图2,若BD是△AOB的外角∠OBE的角平分线,BD与AC相交于点D,点A、B在运动的过程中,∠ADB的大小是否会发生变化?若发生变化,请说明理由;若不发生变化,试求出其值;
(3)如图3,过C作直线与AB交于F,且满足∠AGO-∠BCF=45°,求证:CF∥OB.
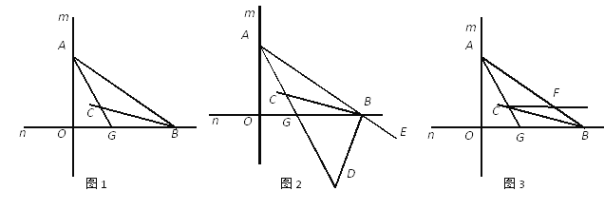
【答案】(1)135°;(2)45°;(3)证明见解析.
【解析】
(1)根据角平分线的性质得到∠OAC =∠CAB,∠ABC=∠GBC,根据三角形的内角和得到∠OAB+∠ABO=90°,即可求出∠CAB+∠ABC的度数,根据三角形的内角和即可求解.
(2)根据角平分线的性质得到∠GBD=∠EBD,则∠CBD=∠GBC+∠GBD=![]() (∠ABG+∠GBE)=90°,根据∠ACB=135°即可求出∠ADB的大小.
(∠ABG+∠GBE)=90°,根据∠ACB=135°即可求出∠ADB的大小.
(3)根据三角形外角的性质得到∠AGO=∠GCB+∠GBC=45°+∠GBC,∠AGO-∠BCF=45°,可得到∠GBC=∠BCF,即可证明.
(1)∵AC、BC分别是∠BAO和∠ABO角的平分线,
∴∠OAC =∠CAB,∠ABC=∠GBC,
∵m⊥n,
∴∠AOB=90°,
∴∠ACB=180°-(∠CAB+∠ABC)
=180°-![]() (∠OAB+∠ABO)=180°-
(∠OAB+∠ABO)=180°-![]() ×90° =135°.
×90° =135°.
(2)∵BD是∠OBE角的平分线,∴∠GBD=∠EBD,
∴∠CBD=∠GBC+∠GBD=![]() (∠ABG+∠GBE)=90°,
(∠ABG+∠GBE)=90°,
又∵∠ACB=135°,∴∠DCB=45°,
∴∠ADB=180°-∠CBD -∠DCB=45°
点A、B在运动的过程中,∠ADB不发生变化,其值为45°.
(3)∵∠AGO=∠GCB+∠GBC=45°+∠GBC,
又已知:∠AGO-∠BCF=45°,
∴ 45°+∠GBC-∠BCF=45°,
∠GBC=∠BCF,∴CF∥OB.


科目:初中数学 来源: 题型:
【题目】如图,将平行四边形ABCD折叠,使顶点D恰落在AB边上的点M处,折痕为AN,那么下列说法不正确的是( )

A. MN∥BCB. MN=AMC. AN=BCD. BM=CN
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c经过△ABC的三个顶点,与y轴相交于(0, ![]() ),点A坐标为(-1,2),点B是点A关于y轴的对称点,点C在x轴的正半轴上.
),点A坐标为(-1,2),点B是点A关于y轴的对称点,点C在x轴的正半轴上.
(1)求该抛物线的函数解析式;
(2)点F为线段AC上一动点,过点F作FE⊥x轴,FG⊥y轴,垂足分别为点E,G,当四边形OEFG为正方形时,求出点F的坐标;
(3)将(2)中的正方形OEFG沿OC向右平移,记平移中的正方形OEFG为正方形DEFG,当点E和点C重合时停止运动,设平移的距离为t,正方形的边EF与AC交于点M,DG所在的直线与AC交于点N,连接DM,是否存在这样的t,使△DMN是等腰三角形?若存在,求t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习了正方形之后,给同桌小文出了道题.从下列四个条件:①AB=BC;②∠ABC=90°;③AC=BD;④AC⊥BD中选出两个作为补充条件,使平行四边形ABCD成为正方形(如图所示).现有下列四种选法,你认为其中错误的是( )

A. ①②B. ②④C. ①③D. ②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知抛物线经过A(﹣4,0),B(0,﹣4),C(2,0)三点.
(1)求抛物线的解析式;
(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S.求S关于m的函数关系式,并求出S的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王晓同学要证明命题“对角线相等的平行四边形是矩形”是正确的,她先作出了如图所示的平行四边形ABCD,并写出了如下不完整的已知和求证.

已知:如图,在平行四边形ABCD中, .
求证:平行四边形ABCD是 .
(1)在方框中填空,以补全已知和求证;
(2)按王晓的想法写出证明过程.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家推行“节能减排,低碳经济”政策后,某环保节能设备生产的产品供不应求,若该企业的某种环保设备每月的产量保持在一定的范围,每套产品的生产成本不高于44万元,每套产品的售价不低于80万元.已知这种设备的月产量x(套)与每套的售价y1(万元)间满足关系式y1=160﹣2x,月产量x(套)与生产总成本y2(万元)存在如图所示的函数关系.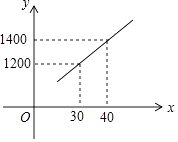
(1)直接写出y2与x之间的函数关系式;
(2)求月产量x的范围;
(3)当月产量x(套)为多少时,这种设备的利润W(万元)最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知n边形的内角和θ=(n-2)×180°.
(1)甲同学说,θ能取360°;而乙同学说,θ也能取630°.甲、乙的说法对吗?若对,求出边数n.若不对,说明理由;
(2)若n边形变为(n+x)边形,发现内角和增加了360°,用列方程的方法确定x.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com