
| 运输工具 | 平均速度(千米/小时) | 运费(元/千米) | 装卸总费用(元) |
| 火车 | 120 | 20 | 2400 |
| 汽车 | 100 | 25 | 1600 |
分析 (1)根据“总运费=运输费+损耗费+装卸费”表示火车和汽车运输的总费;
(2)根据(1)列出两种运送方式的总费用,根据使用的总支出费用一样列方程求解;
(3)设A县与C市的距离为S千米,同理求出两种运输工具的费用,根据相等大于、等于、小于列式得出结论.
解答 解:(1)W1=150×$\frac{x}{120}$+20x+2400=$\frac{85}{4}$x+2400,
W2=150×$\frac{x}{100}$+25x+1600=$\frac{53}{2}$x+1600,
故答案为:$\frac{85}{4}$x+2400,$\frac{53}{2}$x+1600;
(2)由W2-W1=1600得:
$\frac{53}{2}$x+1600-($\frac{85}{4}$x+2400)=1600,
解得:x=$\frac{3200}{7}$,
答:A县与B市之间的路程为$\frac{3200}{7}$千米;
(3)设A县与C市的距离为S千米,
则用火车运输的总费用W1=$\frac{s}{120}$×150+20s+2400=$\frac{85}{4}$s+2400,
用汽车运输的总费用为W2=$\frac{s}{100}$×150+25s+1600=26.5s+1600,
当W1=W2时,$\frac{85}{4}$s+2400=26.5s+1600,
s=$\frac{3200}{21}$,
当W1>W2时,$\frac{85}{4}$s+2400>26.5s+1600,
s<$\frac{3200}{21}$,
当W1<W2时,$\frac{85}{4}$s+2400<26.5s+1600,
s>$\frac{3200}{21}$,
答:①A县与C市的距离为小于$\frac{3200}{21}$千米时,选择汽车运输比较合算;
②A县与C市的距离为等于$\frac{3200}{21}$千米时,选择两种运输费用都一样;
③A县与C市的距离为大于$\frac{3200}{21}$千米时,选择火车运输比较合算.
点评 此题考查的是一元一次方程的应用,关键是列出两种运送方式的总费用得方程或不等式求解.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
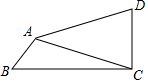 如图,在四边形ABCD中,∠BCD=90°,∠D+2∠B=180°,AD=5,AB=2,CD=3,则AC=$\frac{8\sqrt{10}}{5}$.
如图,在四边形ABCD中,∠BCD=90°,∠D+2∠B=180°,AD=5,AB=2,CD=3,则AC=$\frac{8\sqrt{10}}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
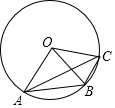 如图,A,B,C是⊙O上三个点,∠AOB=2∠BOC,则下列说法中正确的是( )
如图,A,B,C是⊙O上三个点,∠AOB=2∠BOC,则下列说法中正确的是( )| A. | ∠OBA=∠OCA | B. | 四边形OABC内接于⊙O | ||
| C. | AB=2BC | D. | ∠OBA+∠BOC=90° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com