
【题目】某公交公司有A,B型两种客车,它们的载客量和租金如下表:
A | B | |
载客量(人/辆) | 45 | 30 |
租金(元/辆) | 400 | 280 |
某中学根据实际情况,计划租用A,B型客车共5辆,同时送七年级师生到基地校参加社会实践活动.设租用A型客车x辆,根据要求回答下列问题:
(1)用含x的式子填写下表:
车辆数(辆) | 载客量 | 租金(元) | |
A | x | 45x | 400x |
B | 5-x |
(2)若要保证租车费用不超过1900元,求x的最大值.
【答案】(1)30(5-x);280(5-x);(2)x的最大值为4
【解析】
(1)设租A型客车x辆,则租B型客车(5-x)辆,根据每辆B型客车的载客量及租车费用,即可完成表格数据;
(2)根据总租车费用=租A型客车的费用+租B型客车的费用结合租车费用不超过1900元,即可得出关于x的一元一次不等式,解之取其中的最大整数即可得出结论.
解:(1)设租A型客车x辆,则租B型客车(5-x)辆,
A型客车乘坐学生45x人,B型客车乘坐学生30(5-x)人,租A型客车的总租金为400x元,租B型客车的总租金为280(5-x)元.
故答案为:30(5-x);280(5-x).
(2)根据题意得:400x+280(5-x)≤1900,
解得:x≤![]() .
.
∵x为整数,
∴x≤4.
答:x的最大值为4.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:初中数学 来源: 题型:
【题目】如图,直线CB∥OA,∠C=∠A=112°,E,F在CB上,且满足∠FOB=∠AOB,DE平分∠COF.
(1)求∠EOB的度数;
(2)若平行移动AB,那么∠OBC:∠OFC的值是否随之发生变化?若变化,找出变化规律或求出变化范围;若不变,求出这个比值;
(3)在平行移动AB的过程中,是否存在某种情况使∠OEC=∠OBA?若存在,求出其度数;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的正方形网格中,每个小正方形的边长均为1个单位, ![]() 的三个顶点都在格点上.
的三个顶点都在格点上.
(1)在网格中画出![]() 向下平移3个单位得到的
向下平移3个单位得到的![]() ;
;
(2)在网格中画出![]() 关于直线
关于直线![]() 对称的
对称的![]() ;
;
(3)在直线![]() 上画一点
上画一点![]() ,使得
,使得![]() 的值最大.
的值最大.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了测量被池塘隔开的A,B两点之间的距离,根据实际情况,作出如图所示的图形,其中AB⊥BE,EF⊥BE,AF交BE于点D,C在BD上.有四位同学分别测量出以下4组数据:①BC,∠ACB;②CD,∠ACB,∠ADB;③EF,DE,BD;④DE,DC,BC.能根据所测数据,求出A,B两点之间距离的有( )
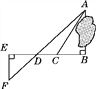
A. 1组 B. 2组 C. 3组 D. 4组
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校开展课外体育活动,决定开展:篮球、乒乓球、踢毽子、跑步四种活动项目.为了解学生最喜欢哪一种活动项目(每人只选取一种).随机抽取了部分学生进行调查,并将调查结果绘成如下统计图,请你结合图中信息解答下列问题.
(1)样本中最喜欢篮球项目的人数所占的百分比为 ,其所在扇形统计图中对应的圆心角度数是 度;
(2)请把条形统计图补充完整;
(3)若该校有学生1000人,请根据样本估计全校最喜欢踢毽子的学生人数约是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,AB=8cm,BC=6cm.动点P、Q分别从点A、B同时开始移动,点P的速度为1 cm/秒,点Q的速度为2 cm/秒,点Q移动到点C后停止,点P也随之停止运动下列时间瞬间中,能使△PBQ的面积为15cm 的是( )
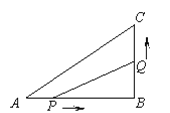
A. 2秒钟 B. 3秒钟 C. 4秒钟 D. 5秒钟
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了抓住梵净山文化艺术节的商机,某商店决定购进A、B两种艺术节纪念品.若购进A种纪念品8件,B种纪念品3件,需要950元;若购进A种纪念品5件,B种纪念品6件,需要800元.
(1)求购进A、B两种纪念品每件各需多少元?
(2)若该商店决定购进这两种纪念品共100件,考虑市场需求和资金周转,用于购买这100件纪念品的资金不少于7500元,但不超过7650元,那么该商店共有几种进货方案?
(3)若销售每件A种纪念品可获利润20元,每件B种纪念品可获利润30元,在第(2)问的各种进货方案中,哪一种方案获利最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“九宫图”传说是远古时代洛河中的一个神龟背上的图案,故又称“龟背图”,中国古代数学史上经常研究这一神话。
⑴现有1,2,3,4,5,6,7,8,9共九个数字,请将它们分别填入图1的九个方格中,使得每行的三个数、每列的三个数、斜对角的三个数之和都等于15.
⑵通过研究问题⑴,利用你发现的规律,将3,5,-7,1,7,-3,9,-5,-1
这九个数字分别填入图2的九个方格中,使得横、竖、斜对角的所有三个数的和都相等.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B分别在射线OM、ON上运动(不与点O重合).
(1)如图1,若∠MON=90°,∠OBA、∠OAB的平分线交于点C,则∠ACB= °;
(2)如图2,若∠MON=n°,∠OBA、∠OAB的平分线交于点C,求∠ACB的度数;
(3)如图2,若∠MON=n°,△AOB的外角∠ABN、∠BAM的平分线交于点D,求∠ACB与∠ADB之间的数量关系,并求出∠ADB的度数;
(4)如图3,若∠MON=80°,BC是∠ABN的平分线,BC的反向延长线与∠OAB的平分线交于点E.试问:随着点A、B的运动,∠E的大小会变吗?如果不会,求∠E的度数;如果会,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com