【题目】每年的6月5日为世界环保日，为了提倡低碳环保，某公司决定购买12台节能新设备，现有甲乙两种型号的设备可供选购，经调查，购4台甲比购3台乙多用18万元，购3台甲比购4台乙少用4万元。
（1）求甲乙两种设备的单价。
（2）该公司决定购买甲设备不少于5台，购买资金不超过136万元，你认为该公司有几种购买方案？并直接写出最省钱的购买方案。
【答案】（1）甲设备每台12万元，乙设备每台10万元；（2）有四种购买方案：①甲5乙7，②甲6乙6，③甲7乙5，④甲8乙4，其中最省钱的方案是甲5乙7.
【解析】
（1）设甲设备的单价为x万元，乙设备的单价为y万元，根据“购4台甲比购3台乙多用18万元，购3台甲比购4台乙少用4万元”，即可得出关于x，y的二元一次方程组，解之即可得出结论；
（2）设购进甲设备m台，则购进乙设备（12-m）台，根据购买甲设备不少于5台且购买资金不超过136万元，即可得出关于m的一元一次不等式组，解之即可得出m的取值范围，结合m为整数可得出各购买方案，再由甲设备的单价＞乙设备的单价可找出最省钱的购买方案．
解：（1）设甲单价为
万元/台，乙为
万元/台，则
，
解得
.
即甲设备每台12万元，乙设备每台10万元.
（2）设购甲
台，由题意得
，
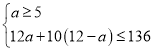解得
.
由为整数得
、6、7、8.
所以有四种购买方案：①甲5乙7，②甲6乙6，③甲7乙5，④甲8乙4，
∵甲设备单价<乙设备单价，
∴其中最省钱的方案是甲5乙7.
浙江名校名师金卷系列答案科目：初中数学 来源： 题型：
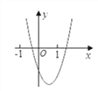
【题目】二次函数y=ax2+bx+c的图象如图,则一次函数y=bx+b2﹣4ac与反比例函数y=
在同一坐标系内的图象大致为（ ）
A. 
B. 
C. 
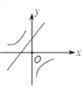D. 
查看答案和解析>>
科目：初中数学 来源： 题型：
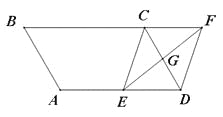
【题目】（7分）如图，平行四边形ABCD中，AB=3cm，BC=5cm，∠B=60°，G是CD的中点，E是边AD上的动点，EG的延长线与BC的延长线交于点F，连接CE，DF．
（1）求证：四边形CEDF是平行四边形；
（2）①当AE= cm时，四边形CEDF是矩形；
②当AE= cm时，四边形CEDF是菱形；（直接写出答案，不需要说明理由）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知A1(1，0)，A2(1，1)，A3(－1，1)，A4(－1，－1)，A5(2，－1)，…，则点A2 019的坐标为____________．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图（1），矩形OABC的边OA、OC在坐标轴上，点B坐标为(5，4)，点P是射线BA上的一动点，把矩形OABC沿着CP折叠，点B落在点D处．
（1）当点C、D、A共线时，AD= ；
（2）如图（2），当点P与点A重合时，CD与x轴交于点E，过点E作EF⊥AC，交BC于点F，请判断四边形AECF的形状，并说明理由；
（3）若点D正好落在x轴上，请直接写出点P的坐标： ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在Rt△ABC中，∠C=90°，P是BC边上不同于B、C的一动点，过P作PQ⊥AB，垂足为Q，连接AP．
（1）试说明不论点P在BC边上何处时，都有△PBQ与△ABC相似；
（2）若Rt△AQP≌Rt△ACP≌Rt△BQP，求tanB的值；
（3）已知AC=3，BC=4，当BP为何值时，△AQP面积最大，并求出最大值.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在菱形
中，
，
，点
是
边的中点，点
是
边上一动点（不与点
重合），延长
交射线
于点
，连接
，
．
（1）求证：四边形
是平行四边形；
（2）填空：
①当
的值为_______时，四边形是矩形；
②当的值为______时，四边形是菱形．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某文具店出售
、
两种文具．文具每套
元，文具每套
元，该店开展促销活动，向客户提供两种优惠方案：
①买一套文具送一套文具．
②文具和文具都按定价的
付款．
现某客户要到该店购买文具
套，文具
套（
）
（
）若该客户按方案①购买需付款____________________元（用含的代数式表示）；若该客户按方案②购买需付款____________________元（用含的代数式表示）
（
）当
时，通过计算说明按哪种方案购买较为合算．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com