
| 1 |
| 2 |
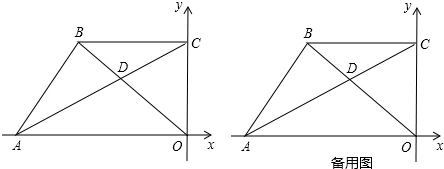
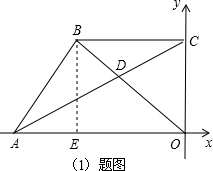 解:如图,过点B作BE⊥OA于E,
解:如图,过点B作BE⊥OA于E,| 1 |
| 2 |
| S△CPQ |
| S△CBA |
| CP |
| CB |
| t2 |
| 25 |
| CP |
| CB |
| CQ |
| CA |
| t |
| 5 |
| t |
| 5 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 5 |
| CD |
| AD |
| CB |
| OA |
| 5 |
| 8 |
| 5 |
| 13 |
| 5 |
| 13 |
| t |
| 5 |
| S△CPQ |
| S△PDQ |
| CQ |
| DQ |
| ||
| S△PDQ |
| ||||
(
|
| 5 |
| 13 |
| t |
| 5 |
| 2 |
| 5 |
| 10 |
| 13 |
| CP |
| CB |
| CD |
| CA |
| t |
| 5 |
| ||
| CA |
| 25 |
| 13 |
| 25 |
| 13 |
| t |
| 5 |
| 5 |
| 13 |
| S△CPQ |
| S△PDQ |
| CQ |
| DQ |
| ||
| S△PDQ |
| ||||
(
|
| t |
| 5 |
| 5 |
| 13 |
| 2 |
| 5 |
| 10 |
| 13 |
| 25 |
| 13 |
| 2 |
| 5 |
| 10 |
| 13 |
| 25 |
| 13 |
| 2 |
| 5 |
| 10 |
| 13 |
| 25 |
| 13 |
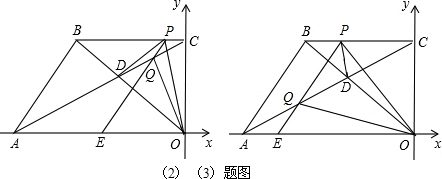
| CP |
| AE |
| t |
| 5-t |
| 4-h |
| h |
| 4 |
| 5 |
| 1 |
| 2 |
| 1 |
| 2 |
| 4 |
| 5 |
| 2 |
| 5 |
| 6 |
| 5 |
| 2 |
| 5 |
| 6 |
| 5 |
| 2 |
| 5 |
| 10 |
| 13 |
| 122 |
| 65 |
| 61 |
| 65 |
| 2 |
| 5 |
| 6 |
| 5 |
| 2 |
| 5 |
| 10 |
| 13 |
| 6 |
| 5 |
| 278 |
| 65 |
| 139 |
| 39 |
| 61 |
| 65 |
| 139 |
| 39 |


科目:初中数学 来源: 题型:
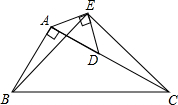 如图,在直角三角形ABC中,∠BAC=90°,AC=2AB,点D是AC的中点,将一块锐角为45°的直角三角板ADE如图放置,使三角板斜边的两个端点分别与A、D重合,连接BE、EC.
如图,在直角三角形ABC中,∠BAC=90°,AC=2AB,点D是AC的中点,将一块锐角为45°的直角三角板ADE如图放置,使三角板斜边的两个端点分别与A、D重合,连接BE、EC.| 5 |
| A、1个 | B、2个 | C、3个 | D、4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:
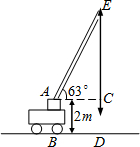 如图所示,一辆吊车的吊臂以63°的倾角倾斜于水平面,如果这辆吊车支点A距地面的高度AB为2m,且点A到铅垂线ED的距离为AC=15m,求吊臂的最高点E到地面的高度ED的长.(sin63°≈0.89,cos63°≈0.45,tan63°≈1.96,精确到0.1m)
如图所示,一辆吊车的吊臂以63°的倾角倾斜于水平面,如果这辆吊车支点A距地面的高度AB为2m,且点A到铅垂线ED的距离为AC=15m,求吊臂的最高点E到地面的高度ED的长.(sin63°≈0.89,cos63°≈0.45,tan63°≈1.96,精确到0.1m)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com