
【题目】请阅读下列材料,并完成相应的任务.
三等分任意角问题是数学史上一个著名的问题,直到1837年,数学家才证明了“三等分任意角”是不能用尺规完成的.
在探索中,出现了不同的解决问题的方法
方法一:
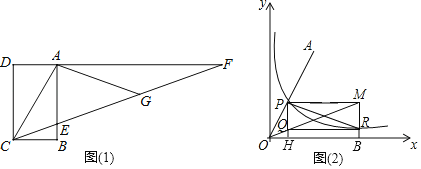
如图(1),四边形ABCD是矩形,F是DA延长线上一点,G是CF上一点,CF与AB交于点E,且∠ACG=∠AGC,∠GAF=∠F,此时∠ECB=![]() ∠ACB.
∠ACB.
方法二:
数学家帕普斯借助函数给出一种“三等分锐角”的方法(如图(2)):将给定的锐角∠AOB置于平面直角坐标系中,边OB在x轴上,边OA与函数y=![]() 的图象交于点P,以点P为圆心,以2OP长为半径作弧交图象于点R.过点P作x轴的平行线,过点R作y轴的平行线,两直线相交于点M,连接OM得到∠AOB,过点P作PH⊥x轴于点H,过点R作RQ⊥PH于点Q,则∠MOB=
的图象交于点P,以点P为圆心,以2OP长为半径作弧交图象于点R.过点P作x轴的平行线,过点R作y轴的平行线,两直线相交于点M,连接OM得到∠AOB,过点P作PH⊥x轴于点H,过点R作RQ⊥PH于点Q,则∠MOB=![]() ∠AOB.
∠AOB.
(1)在“方法一”中,若∠ACF=40°,GF=4,求BC的长.
(2)完成“方法二”的证明.
【答案】(1)2;(2)证明见解析.
【解析】
(1)先求出AC的值再求出∠ACB,利用三角函数即可解答
(2)设点P的坐标为(a,![]() ),点R的坐标为(b,
),点R的坐标为(b,![]() ),则点Q的坐标为(a,
),则点Q的坐标为(a,![]() ),点M的坐标为(b,
),点M的坐标为(b,![]() ),求出直线OM的解析式,得出四边形PQRM为矩形,设PR交MQ于点S,根据SP=SQ=SR=SM=
),求出直线OM的解析式,得出四边形PQRM为矩形,设PR交MQ于点S,根据SP=SQ=SR=SM=![]() PR,即可解答
PR,即可解答
(1)解:∵∠ACG=∠AGC,∠GAF=∠F,
∴AC=AG=GF=4.
∵∠ECB=![]() ∠ACB,∠ACF=40°,
∠ACB,∠ACF=40°,
∴∠ACB=![]() ∠ACF=60°,
∠ACF=60°,
∴BC=ACcos∠ACB=4×![]() =2.
=2.
(2)证明:设点P的坐标为(a,![]() ),点R的坐标为(b,
),点R的坐标为(b,![]() ),则点Q的坐标为(a,
),则点Q的坐标为(a,![]() ),点M的坐标为(b,
),点M的坐标为(b,![]() ).
).
设直线OM的解析式为y=kx(k≠0),
将M(b,![]() )代入y=kx,得:
)代入y=kx,得:![]() =kb,
=kb,
∴k=![]() ,
,
∴直线OM的解析式为y=![]() x.
x.
∵当x=a时,y=![]() ,
,
∴点Q在直线OM上.
∵PH⊥x轴,RQ⊥PH,MP∥x轴,MR∥y轴,
∴四边形PQRM为矩形.
设PR交MQ于点S,如图(2)所示.
则SP=SQ=SR=SM=/span>![]() PR,
PR,
∴∠SQR=∠SRQ.
∵PR=2OP,
∴PS=OP=![]() PR,
PR,
∴∠POS=∠PSO.
∵∠PSQ=2∠SQR,
∴∠POS=2∠SQR.
∵RQ∥OB,
∴∠MOB=∠SQR,
∴∠POS=2∠MOB,
∴∠MOB=![]() ∠AOB.
∠AOB.



 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】 为更新果树品种,某果园计划新购进A、B两个品种的果树苗栽植培育,若计划购进这两种果树苗共45棵,其中A种苗的单价为7元/棵,购买B种苗所需费用y(元)与购买数量x(棵)之间存在如图所示的函数关系.
(1)求y与x的函数关系式;
(2)若在购买计划中,B种苗的数量不超过35棵,但不少于A种苗的数量,请设计购买方案,使总费用最低,并求出最低费用.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某小区居民使用共享单车次数的情况,某研究小组随机采访该小区的10位居民,得到这10位居民一周内使用共享单车的次数统计如下:
使用次数 | 0 | 5 | 10 | 15 | 20 |
人数 | 1 | 1 | 4 | 3 | 1 |
(1)这10位居民一周内使用共享单车次数的中位数是 次,众数是 次,平均数是 次.
(2)若小明同学把数据“20”看成了“30”,那么中位数,众数和平均数中不受影响的是 .(填“中位数”,“众数”或“平均数”)
(3)若该小区有200名居民,试估计该小区居民一周内使用共享单车的总次数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.某商场为缓解“停车难”问题,拟建造地下停车库,如图是该地下停车库坡道入口的设计示意图,其中,AB⊥BD,∠BAD=18°,C在BD上,BC=0.5 m.根据规定,地下停车库坡道入口上方要张贴限高标志,以便告知驾驶员所驾车辆能否安全驶入.小明认为CD的长就是所限制的高度,而小亮认为应该以CE的长作为限制的高度.小明和小亮谁说得对?请你判断并计算出正确的结果.(结果精确到0.1 m,参考数据:sin 18°≈0.31,cos 18°≈0.95,tan 18°≈0.325)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一个矩形的一边是另一边的两倍,则称这个矩形为方形.如图1,矩形![]() 中,
中,![]() ,则称
,则称![]() 为方形.
为方形.

(Ⅰ)设![]() 是方形的一组邻边,写出
是方形的一组邻边,写出![]() 的一组值为__________;
的一组值为__________;
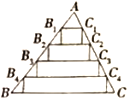
(Ⅱ)在![]() 中,将
中,将![]() 分别五等分,连结两边对应的等分点,以这些连结线为一边作矩形,使得这些矩形的边
分别五等分,连结两边对应的等分点,以这些连结线为一边作矩形,使得这些矩形的边![]() 的对边分别在
的对边分别在![]() 上,如图2所示.
上,如图2所示.
①若![]() ,
,![]() 边上的高为
边上的高为![]() ,判断以
,判断以![]() 为一边的矩形是否是方形?_________(填“是”或“否”);②若以
为一边的矩形是否是方形?_________(填“是”或“否”);②若以![]() 为一边的矩形为方形,则
为一边的矩形为方形,则![]() 与
与![]() 边上的高之比为__________.
边上的高之比为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点E是正方形ABCD边CD上任意一点,以DE为边作正方形DEFG,连接BF,点M是线段BF中点,射线EM与BC交于点H,连接CM.
(1)请直接写出CM和EM的数量关系和位置关系;
(2)把图1中的正方形DEFG绕点D顺时针旋转45°,此时点F恰好落在线段CD上,如图2,其他条件不变,(1)中的结论是否成立,请说明理由;
(3)把图1中的正方形DEFG绕点D顺时针旋转90°,此时点E、G恰好分别落在线段AD、CD上,如图3,其他条件不变,(1)中的结论是否成立,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一种适用于笔记本电脑的铝合金支架,边![]() ,
,![]() 可绕点
可绕点![]() 开合,在
开合,在![]() 边上有一固定点
边上有一固定点![]() ,支柱
,支柱![]() 可绕点
可绕点![]() 转动,边
转动,边![]() 上有六个卡孔,其中离点
上有六个卡孔,其中离点![]() 最近的卡孔为
最近的卡孔为![]() ,离点
,离点![]() 最远的卡孔为
最远的卡孔为![]() .当支柱端点
.当支柱端点![]() 放入不同卡孔内,支架的倾斜角发生变化.将电脑放在支架上,电脑台面的角度可达到六档调节,这样更有利于工作和身体健康.现测得
放入不同卡孔内,支架的倾斜角发生变化.将电脑放在支架上,电脑台面的角度可达到六档调节,这样更有利于工作和身体健康.现测得![]() 的长为
的长为![]() ,
,![]() 为
为![]() ,支柱
,支柱![]() 为
为![]() .
.

(1)当支柱的端点![]() 放在卡孔
放在卡孔![]() 处时,求
处时,求![]() 的度数;
的度数;
(2)当支柱的端点![]() 放在卡孔
放在卡孔![]() 处时,
处时,![]() ,若相邻两个卡孔的距离相同,求此间距.(结果精确到十分位)
,若相邻两个卡孔的距离相同,求此间距.(结果精确到十分位)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com