
 如图,在△ABC中,AB=AC,∠BAC=45°,AE是∠BAC的平分线,CD⊥AB于D,交AE于点F.请探索AF与BC之间的数量关系,并说明理由.
如图,在△ABC中,AB=AC,∠BAC=45°,AE是∠BAC的平分线,CD⊥AB于D,交AE于点F.请探索AF与BC之间的数量关系,并说明理由. 分析 先求出∠ACD=180°-∠DAC-∠ADC=45°,那么∠ACD=∠DAC=45°,根据等角对等边得出AD=CD.再证明∠DAF=∠DCB=22.5°,从而根据ASA证明△ADF≌△CDB,得出AF=BC.
解答 解:AF=BC.理由如下:
∵∠BAC=45°,CD⊥AB于D,
∴∠ACD=180°-∠DAC-∠ADC=180°-45°-90°=45°,
∴∠ACD=∠DAC=45°,
∴AD=CD.
∵在△ABC中,AB=AC,∠BAC=45°,AE是∠BAC的平分线,
∴∠BAE=∠CAE=$\frac{1}{2}$∠BAC=22.5°,∠ACB=∠B=$\frac{1}{2}$(180°-45°)=67.5°,
∴∠BCD=∠ACB-∠ACD=67.5°-45°=22.5°.
在△ADF与△CDB中,
$\left\{\begin{array}{l}{∠DAF=∠DCB=22.5°}\\{AD=CD}\\{∠ADF=∠CDB=90°}\end{array}\right.$,
∴△ADF≌△CDB,
∴AF=BC.
点评 本题考查了等腰三角形的性质,等腰直角三角形的判定与性质,全等三角形的判定与性质,三角形内角和定理,证明出AD=CD以及∠DAF=∠DCB是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
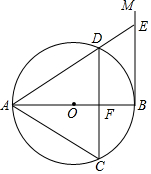 如图,AB是⊙O的直径,过点B作⊙O的切线BM,弦CD∥BM,交AB于点F,且 $\widehat{DA}$=$\widehat{DC}$,连结AC、AD,延长AD交BM于点E.
如图,AB是⊙O的直径,过点B作⊙O的切线BM,弦CD∥BM,交AB于点F,且 $\widehat{DA}$=$\widehat{DC}$,连结AC、AD,延长AD交BM于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
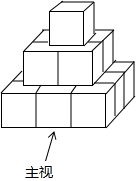 把棱长为1cm的若干个小正方体摆成如图所示的立体图形,然后在露出的表面上涂上颜色(不含底面).
把棱长为1cm的若干个小正方体摆成如图所示的立体图形,然后在露出的表面上涂上颜色(不含底面).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
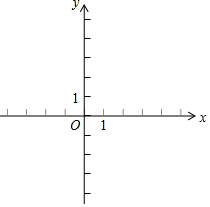 已知抛物线y=$\frac{1}{2}$x2-x-4与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,过点C作直线1∥x轴.将该抛物线在y轴左侧的部分沿直线1翻折,抛物线的其余部分保持不变.得到一个新的图象,记为G.请你结合图象问答:当直线y=$\frac{1}{2}$x+b与图象G只有一个公共点时,求b的取值范围.
已知抛物线y=$\frac{1}{2}$x2-x-4与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,过点C作直线1∥x轴.将该抛物线在y轴左侧的部分沿直线1翻折,抛物线的其余部分保持不变.得到一个新的图象,记为G.请你结合图象问答:当直线y=$\frac{1}{2}$x+b与图象G只有一个公共点时,求b的取值范围.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
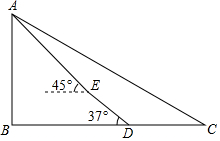 今年国庆节,小明与爸爸一起去省级风景名胜区彭祖山游览,小明想估算彭祖山AB的高度,如图,他在距山脚下400米的C点测得山顶的仰角为30°,来到山脚下D点,沿37°斜坡DE走400米到彭祖墓前,测得山顶的仰角为45°,请你帮助小明估算一下彭祖山的高度.(结果精确到1m)(参考数据:$\sqrt{3}$=1.732,$\sqrt{2}$=1.414,sin37°=0.6,cos37°=0.8,tan37°=0.75,cot37°=1.33)
今年国庆节,小明与爸爸一起去省级风景名胜区彭祖山游览,小明想估算彭祖山AB的高度,如图,他在距山脚下400米的C点测得山顶的仰角为30°,来到山脚下D点,沿37°斜坡DE走400米到彭祖墓前,测得山顶的仰角为45°,请你帮助小明估算一下彭祖山的高度.(结果精确到1m)(参考数据:$\sqrt{3}$=1.732,$\sqrt{2}$=1.414,sin37°=0.6,cos37°=0.8,tan37°=0.75,cot37°=1.33)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com