
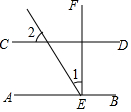
 如图,AB∥CD,EF⊥AB于E,已知∠1=35°,则∠2=55°.
如图,AB∥CD,EF⊥AB于E,已知∠1=35°,则∠2=55°.  小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案科目:初中数学 来源: 题型:解答题
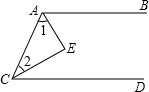 如图,∠BAE=∠DCE=45°,AE⊥CE,通过填空,把下列推理过程补充完整.
如图,∠BAE=∠DCE=45°,AE⊥CE,通过填空,把下列推理过程补充完整.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
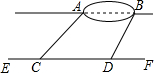 某兴趣小组想测量位于一池塘两端的A、B之间的距离,组长小明带领小组成员沿着与直线AB平行的道路EF行走,当行走到点C处,测得∠ACF=45°,再向前行走100米到达点D处,测得∠BDF=60°,已知AB与EF之间的距离为60米,求A、B两点的距离.
某兴趣小组想测量位于一池塘两端的A、B之间的距离,组长小明带领小组成员沿着与直线AB平行的道路EF行走,当行走到点C处,测得∠ACF=45°,再向前行走100米到达点D处,测得∠BDF=60°,已知AB与EF之间的距离为60米,求A、B两点的距离.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,正方形ABCD中,E为BC的中点,CG⊥DE于G,BG延长交CD于点F,CG延长交BD于点H,AB于N.下列结论:①DE=CN;②∠DGF=45°;③2BN=3CF;④CH+BH=DE.其中正确的有( )
如图,正方形ABCD中,E为BC的中点,CG⊥DE于G,BG延长交CD于点F,CG延长交BD于点H,AB于N.下列结论:①DE=CN;②∠DGF=45°;③2BN=3CF;④CH+BH=DE.其中正确的有( )| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com