
【题目】阅读材料,回答下列问题:
阿尔花拉子米(约780~约850),著名阿拉伯数学家、天文学家、地理学家,是代数与算术的整理者,被誉为“代数之父”.他利用正方形图形巧妙解出了一元二次方程x2+2x﹣35=0的一个解.
将边长为x的正方形和边长为1的正方形,外加两个长方形,长为x,宽为1,拼合在一起面积就是x2+2×1+1×1,即x2+2x+1,而由原方程x2+2x﹣35=0变形得x2+2x+1=35+1,即右边边长为x+1的正方形面积为36.所以(x+1)2=36,则x=5.
(1)上述求解过程中所用的方法与下列哪种方法是一致的 .
A.直接开平方法 B.公式法
C.配方法 D.因式分解法
(2)所用的数学思想方法是 .
A.分类讨论思想 B.数形结合思想 C.转化思想
(3)运用上述方法构造出符合方程x2+4x﹣5=0的一个正根的正方形.

科目:初中数学 来源: 题型:
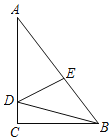
【题目】在Rt△ABC中,∠ACB=90°,AC=8,BC=6,点D、E分别在AC、AB上,且△ADE是直角三角形,△BDE是等腰三角形,则BE=_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一个钝角△ABC(其中∠ABC=120°)绕点B顺时针旋转得△A1BC1,使得C点落在AB的延长线上的点C1处,连接AA1.

(1)写出旋转角的度数;
(2)求证:∠A1AC=∠C1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,点M在BC边上,且BM=![]() BC,AM与BD相交于点N,那么S△BMN:S平行四边形ABCD为( )
BC,AM与BD相交于点N,那么S△BMN:S平行四边形ABCD为( )

A.1:3B.1:9C.1:12D.1:24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,动点P以
,动点P以![]() 的速度从A点出发,沿
的速度从A点出发,沿![]() 向C点移动,同时动点Q以
向C点移动,同时动点Q以![]() 的速度从点C出发,沿
的速度从点C出发,沿![]() 向点B移动,设P、Q两点移动的时间为t秒
向点B移动,设P、Q两点移动的时间为t秒![]() .
.

(1)t为多少时,以P、Q、C为顶点的三角形与![]() 相似?
相似?
(2)在P、Q两点移动过程中,四边形![]() 与
与![]() 的面积能否相等?若能,求出此时t的值;若不能,请说明理由.
的面积能否相等?若能,求出此时t的值;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD的外接圆为⊙O,AD是⊙O的直径,过点B作⊙O的切线,交DA的延长线于点E,连接BD,且∠E=∠DBC.

(1)求证:DB平分∠ADC;
(2)若EB=10,CD=9,tan∠ABE=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中点,将
的中点,将![]() 绕点
绕点![]() 旋转,当
旋转,当![]() (即
(即![]() )与
)与![]() 交于一点
交于一点![]() ,
,![]() (
(![]() )同时与
)同时与![]() 交于一点
交于一点![]() 时,点
时,点![]() ,
,![]() 和点
和点![]() 构成
构成![]() ,在此过程中,
,在此过程中,![]() 周长的最小值是__________.
周长的最小值是__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于的一元二次方程x2+2x+k+1=0的实数解是x1和x2.
(1)求k的取值范围;
(2)如果x1+x2﹣x1x2<﹣1且k为整数,求k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com