
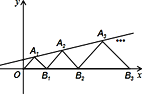
【题目】如图,在平面直角坐标系中,点A1,A2,A3,… 和B1,B2,B3,… 分别在直线![]() 和x轴上.△OA1 B1,△B1 A2 B2,△B2 A3 B3,…都是等腰直角三角形.如果点A1(1,1),那么点A2019的纵坐标是( )
和x轴上.△OA1 B1,△B1 A2 B2,△B2 A3 B3,…都是等腰直角三角形.如果点A1(1,1),那么点A2019的纵坐标是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
因为每个A点为等腰直角三角形的直角顶点,则每个点A的纵坐标为对应等腰直角三角形的斜边一半.故先设出各点A的纵坐标,可以表示A的横坐标,代入解析式可求点A的纵坐标,规律可求.
分别过点A1,A2,A3,…向x轴作垂线,垂足为C1,C2,C3,…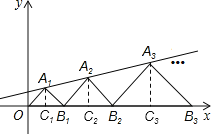
∵点A1(1,1)在直线y=![]() x+b上
x+b上
∴代入求得:b=![]()
∴y=![]()
∵△OA1B1为等腰直角三角形
∴OB1=2
设点A2坐标为(a,b)
∵△B1A2B2为等腰直角三角形
∴A2C2=B1C2=b
∴a=OC2=OB1+B1C2=2+b
把A2(2+b,b)代入y=![]()
解得b=![]()
∴OB2=5
同理设点A3坐标为(a,b)
∵△B2A3B3为等腰直角三角形
∴A3C3=B2C3=b
∴a=OC3=OB2+B2C3=5+b
把A3(5+b,b)代入y=![]()
解得b=![]()
以此类推,发现每个A的纵坐标依次是前一个的![]() 倍
倍
则A2019的纵坐标是(![]() )2018
)2018
故选:B


科目:初中数学 来源: 题型:
【题目】某商场试销一种成本为每件![]() 元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于成本的
元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于成本的![]() ,经试销发现:销售量
,经试销发现:销售量![]() (件)与销售单价
(件)与销售单价![]() (元)符合一次函数
(元)符合一次函数![]() ,且当
,且当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
(1)求![]() 与
与![]() 之间的函数表达式.
之间的函数表达式.
(2)在试销期间,若该商场获得利润为![]() 元,写出利润
元,写出利润![]() 与销售单价
与销售单价![]() 之间的关系式,并求出利润是
之间的关系式,并求出利润是![]() 元时的销售单价.
元时的销售单价.
(3)在试销期间,销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
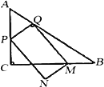
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发,沿折线
出发,沿折线![]() 以每秒
以每秒![]() 个单位长度的速度向终点
个单位长度的速度向终点![]() 运动。当点
运动。当点![]() 不与点
不与点![]() 、
、![]() 重合时,在边
重合时,在边![]() 上取一点
上取一点![]() ,满足
,满足![]() ,过点
,过点![]() 作
作![]() ,交边
,交边![]() 于点
于点![]() ,以
,以![]() 、
、![]() 为边做矩形
为边做矩形![]() .设点
.设点![]() 的运动时间为
的运动时间为![]() 秒.
秒.
(1)用含![]() 的代数式表示线段
的代数式表示线段![]() 的长;
的长;
(2)当矩形![]() 为正方形时,求
为正方形时,求![]() 的值;
的值;
(3)设矩形![]() 与
与![]() 重叠部分图形的周长为
重叠部分图形的周长为![]() ,求
,求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(4)作点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() ,作点
,作点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() .当
.当![]() 、
、![]() 这两点中只有一个点在矩形
这两点中只有一个点在矩形![]() 内部时,直接写出此时
内部时,直接写出此时![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,CE是外角平分线,点D在AC上,连结BD并延长与CE交于点E.
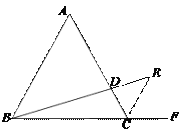
(1)求证:△ABD∽△CED.
(2)若AB=6,AD=2CD,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
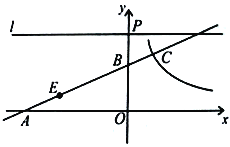
【题目】已知:如图,直线![]() 与
与![]() 轴负半轴交于点
轴负半轴交于点![]() ,与
,与![]() 轴正半轴交于点
轴正半轴交于点![]() ,线段
,线段![]() 的长是方程
的长是方程![]() 的一个根,请解答下列问题:
的一个根,请解答下列问题:
(1)求点![]() 的坐标;
的坐标;
(2)双曲线![]() 与直线
与直线![]() 交于点
交于点![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
(3)在(2)的条件下,点![]() 在线段
在线段![]() 上,
上,![]() ,直线
,直线![]() 轴,垂足为
轴,垂足为![]() ,点
,点![]() 在直线
在直线![]() 上,在直线
上,在直线![]() 上的坐标平面内是否存在点
上的坐标平面内是否存在点![]() ,使以点
,使以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是矩形?若存在,请求出点
为顶点的四边形是矩形?若存在,请求出点![]() 的坐标;若不存在,请说明理由。
的坐标;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
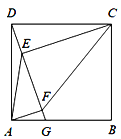
【题目】如图,在正方形ABCD中,点G在边AB上(不与点A,B重合),连接DG,作CE⊥DG于点E,AF⊥DG于点F,连接AE,CF.
(1)求证:DE=AF;
(2)若![]() 设
设![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等式![]() .
.
![]() 若等式中,已知
若等式中,已知![]() 是非零常量,请写出因变量
是非零常量,请写出因变量![]() 与自变量
与自变量![]() 的函数解析式;当
的函数解析式;当![]() 时,求
时,求![]() 的最大值和最小值及对应的
的最大值和最小值及对应的![]() 的取值.
的取值.
![]() 若等式中,
若等式中,![]() 是非零常量,请写出因变量
是非零常量,请写出因变量![]() 与自变量
与自变量![]() 的函数解析式,并判断
的函数解析式,并判断![]() 在什么范围内取值时,
在什么范围内取值时,![]() 随
随![]() 的增大而增大.
的增大而增大.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD放置在平面直角坐标系xOy中,已知A(-2,0),B(2,0),D(0,3),反比例函数y=![]() (x>0)的图象经过点C.
(x>0)的图象经过点C.
(1)求此反比例函数的解析式;
(2)问将平行四边形ABCD向上平移多少个单位,能使点B落在双曲线上?
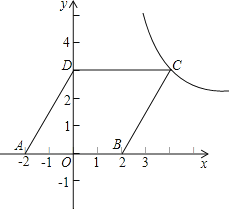
查看答案和解析>>
科目:初中数学 来源: 题型:
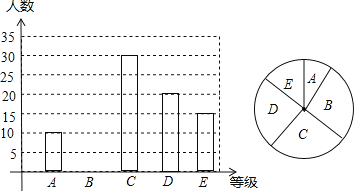
【题目】2019年,我省中考体育分值增加到55分,其中女生必考项目为八百米跑,我校现抽取九年级部分女生进行八百米测试成绩如下:
成绩 | 3′40″及以下 | 3′41~4′ | 4′01″~4′20′ | 4′21″~4′40″ | 4′41″及以上 |
等级 | A | B | C | D | E |
百分比 | 10% | 25% | m | 20% | n |
(1)求样本容量及表格中的m和n的值
(2)求扇形统计图中A等级所对的圆心角度数,并补全统计图.
(3)我校9年级共有女生500人.若女生八百米成绩的达标成绩为4分,我校九年级女生八百米成绩达标的人数有多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com