
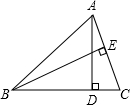
 如图,在△ABC中,AD、BE分别是BC、AC上的高,BC=9,AC=6.求:
如图,在△ABC中,AD、BE分别是BC、AC上的高,BC=9,AC=6.求:分析 (1)根据三角形的面积公式得出$\frac{1}{2}$BC•AD=$\frac{1}{2}$AC•BE,再把AC和BC的值代入即可得出△ABC的高AD与BE的比;
(2)根据(1)的结论代入BE=8,即可得到结论.
解答 解:(1)∵S△ABC=$\frac{1}{2}$BC•AD=$\frac{1}{2}$AC•BE,AC=6,BC=9,
∴$\frac{1}{2}$×9•AD=$\frac{1}{2}$×6•BE,
∴3AD=2BE,
∴$\frac{AD}{BE}$=$\frac{2}{3}$;
(2)由(1)得$\frac{AD}{BE}$=$\frac{2}{3}$,
∵BE=8,
∴AD=$\frac{16}{3}$.
点评 此题考查了比例线段和三角形的面积,利用两个底边和对应的高线列出面积的表达式是解题的关键.


科目:初中数学 来源: 题型:解答题
 如图,Rt△ABC中,AB=AC,∠BAC=90°,直线AE是经过点A的任一直线,BD⊥AE于D,CE⊥AE于E,若BD>CE,试解答:
如图,Rt△ABC中,AB=AC,∠BAC=90°,直线AE是经过点A的任一直线,BD⊥AE于D,CE⊥AE于E,若BD>CE,试解答:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 一辆汽车和一辆摩托车同时分别从A,B两地去同一城市,它们离A地的路程随时间变化的图象如图所示.当汽车到达目的地时,摩托车距目的地20千米.
一辆汽车和一辆摩托车同时分别从A,B两地去同一城市,它们离A地的路程随时间变化的图象如图所示.当汽车到达目的地时,摩托车距目的地20千米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com