
【题目】如图,矩形ABCD中,对角线AC的垂直平分线EF分别交BC,AD于点E,F,若BE=3,AF=5,则AC的长为( )

A. ![]() B.
B. ![]() C. 10D. 8
C. 10D. 8
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数的图象经过P(2,2),顶点为O(0,0),将该图象向右平移,当它再次经过点P时,所得抛物线的函数表达式为( )
A.y=![]() x2B.y=
x2B.y=![]() (x﹣2)2C.y=
(x﹣2)2C.y=![]() (x﹣4)2D.y=
(x﹣4)2D.y=![]() (x﹣2)2+2
(x﹣2)2+2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一条弧经过一个多边形相邻两边中点,并且该弧上所有点都在该多边形的内部或边上,则称该弧为此两边中点连线的EVA弧.例如,图1中,在△ABC中,D,E分别是△ABC两边的中点,如果![]() 上的所有点都在△ABC的内部或边上,则称
上的所有点都在△ABC的内部或边上,则称![]() 为DE的一条EVA弧.
为DE的一条EVA弧.
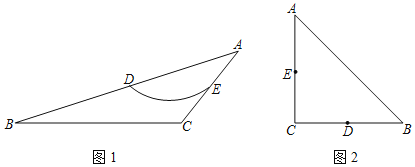
(1)如图2,在Rt△ABC中,∠C=90°,AC=BC=4![]() ,D,E分别是BC,AC的中点,画出DE的最长的EVA弧
,D,E分别是BC,AC的中点,画出DE的最长的EVA弧![]() ,并直接写出此时
,并直接写出此时![]() 的长;
的长;
(2)在平面直角坐标系中,已知点A(0,4),B(0,0),C(4t,0)(t>0),在△ABC中,D,E分别是AB,AC的中点.
①若t=1,求DE的EVA弧![]() 所在圆的圆心P的纵坐标m的取值范围;
所在圆的圆心P的纵坐标m的取值范围;
②若在△ABC中存在一条DE的EVA弧![]() ,使得
,使得![]() 所在圆的圆心P在△ABC的内部或边上,直接写出t的取值范围.
所在圆的圆心P在△ABC的内部或边上,直接写出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的布袋里装有4个标号为1、2、3、4的小球,它们的材质、形状、大小完全相同,小亮从布袋里随机摸出一个小球,记下数字为x,小刚从剩下的3个小球中随机摸出一个小球,记下数字为y,这样确定了点P的坐标(x,y).
(1)若小亮摸出的小球上的数字是2,那么小刚摸出的小球上的数字是4的概率是多少?
(2)利用画树状图或列表格的方法,求点P(x,y)在函数y=﹣x+6的图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】聪明好学的亮亮看到一课外书上有个重要补充:
(角平分线定理)三角形一个内角的平分线分对边所成的两条线段与这个角的两邻边对应成比例.于是他就和其他同学研究一番,写出了已知、求证如下:
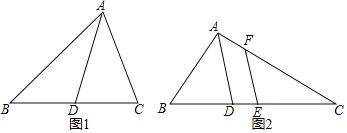
“已知:如图1,△ABC中,AD平分∠BAC交BC于点D,求证:![]() ”
”
可是他们依然找不到证明的方法,于是,老师提示:过点B作BE∥AC交AD延长线于点E,于是得到△BDE∽△CDA,从而打开思路.
(Ⅰ)请你按老师的提示或你认为其他可行的方法帮亮亮完成证明.
(Ⅱ)利用角平分线定理解决如下问题:
如图2,△ABC中,E是BC中点,AD是∠BAC的平分线,EF∥AD交AC于F,AB=7,AC=15,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学数学兴趣小组在一次课外学习与探究中遇到一些新的数学符号,他们将其中某些材料摘录如下:
对于三个实数a,b,c,用M{a,b,c}表示这三个数的平均数,用min{a,b,c}表示这三个数中最小的数,例如M{1,2,9}=![]() =4,min{1,2,﹣3}=﹣3,min(3,1,1)=1.请结合上述材料,解决下列问题:
=4,min{1,2,﹣3}=﹣3,min(3,1,1)=1.请结合上述材料,解决下列问题:
(1)①M{(﹣2)2,22,﹣22}= .②min{2![]() ,3
,3![]() ,4}= .
,4}= .
(2)若min(3﹣2x,1+3x,﹣5)=﹣5,则x的取值范围为 .
(3)若M{﹣2x,x2,3}=2,求x的值.
(4)如果M{2,1+x,2x}=min{2,1+x,2x},求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
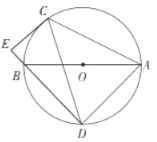
【题目】如图,AB为⊙O的直径,C、D为⊙O上异于A、B的两点,连接CD,过点C作CE⊥DB,交DB的延长线于点E.
(1)连接AC、AD,求证:∠DAC+∠ACE=180°.
(2)若∠ABD=2∠BDC,求证:CE是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
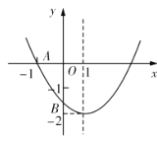
【题目】如图,已知二次函数![]()
![]() 的图像与
的图像与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴的交点
轴的交点![]() 在
在![]() 和
和![]() 之间(不包括这两点),对称轴为直线
之间(不包括这两点),对称轴为直线![]() .下列结论:
.下列结论:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() .
.
其中正确结论有 __________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E在边CD上(不与点C,D重合),连接AE,BD交于点F.
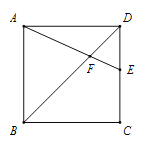
(1)若点E为CD中点,AB=2![]() ,求AF的长.
,求AF的长.
(2)若![]() ∠AFB=2,求
∠AFB=2,求![]() 的值.
的值.
(3)若点G在线段BF上,且GF=2BG,连接AG,CG,设![]() =x,四边形AGCE的面积为
=x,四边形AGCE的面积为![]() ,
,![]() ABG的面积为
ABG的面积为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com