练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    18．若关于x的不等式2x-m＜0仅有两个正整数解，则m的取值范围是4＜m≤6．

    分析 根据题目中的不等式可以求得它的解集，再根据关于x的不等式2x-m＜0仅有两个正整数解，从而可以求得m的取值范围．

    解答 解：2x-m＜0，
    解得，x＜$\frac{m}{2}$，
    ∵关于x的不等式2x-m＜0仅有两个正整数解，
    ∴$2＜\frac{m}{2}≤3$，
    解得，4＜m≤6，
    故答案为：4＜m≤6．

    点评 本题考查一元一次不等式的整数解，解答本题的关键是明确解不等式的方法．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    8．（1）因式分解：（x-8）（x+2）+6x
    （2）解不等式组$\left\{\begin{array}{l}{5x-2＞3（x+1）}\\{\frac{1}{2}x-3≤5-\frac{3}{2}x}\end{array}\right.$，并写出它的整数解．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．将点P（2，1）向左平移2个单位后得到P′，则P′的坐标是（　　）
    A．（2，3）B．（2，-1）C．（4，1）D．（0，1）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．不等式：-1＜$\frac{3x+4}{5}$≤2的非正整数解个数有3个．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    13．下列二次根式不能与$\sqrt{27}$合并的是（　　）
    A．$\sqrt{48}$B．$\sqrt{18}$C．$\sqrt{1\frac{1}{3}}$D．$-\sqrt{75}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

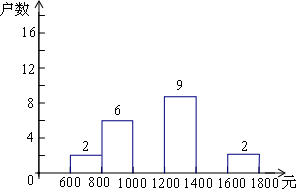    3．小明在学校组织的社会调查活动中负责了解他所居住的小区560户居民的家庭收入情况．他从中随机调查了一定户数的家庭收入情况（收入取整数，单位：元），并绘制了如下的频数分布表和频数分布直方图．
    分组频数百分比
    600≤x＜80025%
    800≤x＜1000615%
    1000≤x＜1200a40%
    1200≤x＜1400922.5%
    1400≤x＜1600bc
    1600≤x＜180025%
    合计40100%
    根据以上提供的信息，解答下列问题：
    （1）频数分布表中：a=16，b=5，c=12.5%．
    （2）补全频数分布直方图．
    （3）请估计该居民小区家庭属于中等收入（大于1000不足1600元）的大约有多少户？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    10．不等式2（x-2）≤x-1的非负整数解的个数为（　　）
    A．1个B．2个C．3个D．4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    7．若点P（2m+4，m-3）在第四象限内，则m的取值范围是（　　）
    A．m＞3B．m＜-2C．-2＜m＜3D．无解

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

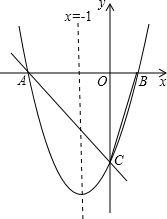    14．如图，对称轴为直线x=-1的抛物线y=ax2+bx+c（a≠0）与x轴相交于A、B两点，其中点A的坐标为（-3，0）．
    （1）求点B的坐标；
    （2）已知a=1，C为抛物线与y轴的交点，若点P在抛物线上，且S△POC=4S△BOC．求点P的坐标．

    查看答案和解析>>

    同步练习册答案