
【题目】有一科技小组进行了机器人行走性能试验,在试验场地有A、B、C三点顺次在同一笔直的赛道上,甲、乙两机器人分别从A、B两点同时同向出发,历时7min同时到达C点,甲机器人前3分钟以a m/min的速度行走,乙机器人始终以60m/min的速度行走,如图是甲、乙两机器人之间的距离y(m)与他们的行走时间x(min)之间的函数图象,请结合图象,回答下列问题:
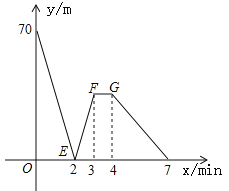
(1)A、B两点之间的距离是____m,A、C两点之间的距离是____m,a=____m/min;
(2)求线段EF所在直线的函数解析式;
(3)设线段FG∥x轴.
①当3≤x≤4时,甲机器人的速度为____m/min;
②直接写出两机器人出发多长时间相距28m.
【答案】(1)70;490;95;(2)y=35x-70;(3)①60;②两机器人出发1.2min、2.8min或4.6min时相距28m.
【解析】
(1)根据图象可直接读出A、B两点间的距离;A、C两点间的距离=A、B两点间的距离+B、C两点间的距离,代入计算即得;先求出甲在2分钟所走的路程=70+60×2,根据速度=路程÷时间,即可求出a.
(2)结合(1)中数据,计算1×(95-60)=35,所以可得点F(3,35),设线段EF所在直线的函数解析式为y=kx+b,然后将点E、F坐标代入解析式中,解出k 、b的值即得.
(3)①由线段FG∥x轴,可得在FG这段时间内甲、乙的速度相等,即得3≤x≤4时的速度.
②分三种情况讨论:当0≤x≤2时,根据70-甲行路程+乙行路程=28列出方程,解出即得;当2<x≤3时,甲行路程-70-乙行路程=28列出方程,解出即得;当4<x≤7时,先求出直线EF的解析式,然后令y=28,解出x即得.
解:(1)由图象,得A、B两点之间的距离是70m,A、C两点间的距离为70+60×7=490(m),a=(70+60×2)÷2=95(m/min).
故答案为70;490;95.
(2)解:由题意,得点F的坐标为(3,35),设线段EF所在直线的函数解析式为y=kx+b,把E、F的坐标代入解析式,可得 ![]() ,
,
解得 ![]() ,
,
即线段EF所在直线的函数解析式是y=35x-70.
(3)①线段FG∥x轴,
∴在FG这段时间内甲、乙的速度相等,
∴当3≤x≤4时,甲机器人的速度为60m/min.
②当0≤x≤2时,则70-(95-60)x=28,得x=1.2;
当2<x≤3时,则95x-70-60x=28,得x=2.8;
当4<x≤7时,设甲、乙两机器人之间的距离y(m)与他们的行走时间x(min)之间函数关系式为y=mx+n,  ,
,
即y=-![]() x+
x+![]() ,
,
令y=28,得28=-![]() x+
x+![]() ,解得x=4.6,
,解得x=4.6,
答:两机器人出发1.2min、2.8min或4.6min时相距28m.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
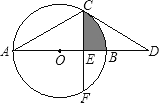
【题目】如图,AB为⊙O的直径,点C在⊙O上,过点C作⊙O的切线交AB的延长线于点D,已知∠D=30°.
(1)求∠A的度数;
(2)若点F在⊙O上,CF⊥AB,垂足为E,CF=![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《小猪佩奇》这部动画片,估计同学们都非常喜欢.周末,小猪佩奇一家4口人(小猪佩奇,小猪乔治,小猪妈妈,小猪爸爸)到一家餐厅就餐,包厢有一圆桌,旁边有四个座位(![]() ,
,![]() ,
,![]() ,
,![]() ).
).


(1)小猪佩奇随机坐到![]() 座位的概率是________;
座位的概率是________;
(2)若现在由小猪佩奇,小猪乔治两人先后选座位,用树状图或列表的方法计算出小猪佩奇和小猪乔治坐对面的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,![]() 的直径
的直径![]() ,点
,点![]() 是
是![]() 延长线上的一点,过
延长线上的一点,过![]() 点作
点作![]() 的切线,切点为
的切线,切点为![]() ,连接
,连接![]() .
.

(1)若![]() ,求
,求![]() 的长;
的长;
(2)若点![]() 在
在![]() 的延长线上运动,
的延长线上运动,![]() 的平分线交
的平分线交![]() 于点
于点![]() ,你认为
,你认为![]() 的大小是否发生变化?若变化,请说明理由;若不变化,求出
的大小是否发生变化?若变化,请说明理由;若不变化,求出![]() 的大小.
的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,∠ACB=90°,BC=3,AC=4,小红按如下步骤作图:
①分别以A、C为圆心,以大于![]() AC的长为半径在AC两边作弧,交于两点M、N;
AC的长为半径在AC两边作弧,交于两点M、N;
②连接MN,分别交AB、AC于点D、O;
③过C作CE∥AB交MN于点E,连接AE、CD.
则四边形ADCE的周长为( )

A. 10 B. 20 C. 12 D. 24
查看答案和解析>>
科目:初中数学 来源: 题型:
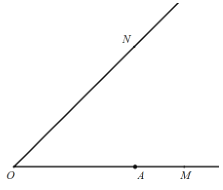
【题目】如图,已知![]() ,
,![]() 为射线
为射线![]() 上一定点,点
上一定点,点![]() 关于射线
关于射线![]() 的对称点为点
的对称点为点![]() 为射线
为射线![]() 上一动点,连接
上一动点,连接![]() ,满足
,满足![]() 为钝角,以点
为钝角,以点![]() 为中心,将线段
为中心,将线段![]() 逆时针旋转
逆时针旋转![]() 至线段
至线段![]() ,满足点
,满足点![]() 在射线
在射线![]() 的反向延长线上.
的反向延长线上.
(1)依题意补全图形;
(2)当点![]() 在运动过程中,旋转角
在运动过程中,旋转角![]() 是否发生变化?若不变化,请求出
是否发生变化?若不变化,请求出![]() 的值,若变化,请说明理由;
的值,若变化,请说明理由;
(3)从点![]() 向射线
向射线![]() 作垂线,与射线
作垂线,与射线![]() 的反向延长线交于点
的反向延长线交于点![]() ,探究线段
,探究线段![]() 和
和![]() 的数量关系并证明.
的数量关系并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为调查某市市民上班时最常用的交通工具的情况,随机抽取了部分市民进行调查,要求被调查者从“![]() :自行车,
:自行车,![]() :家庭汽车,
:家庭汽车,![]() :公交车,
:公交车,![]() :电动车,
:电动车,![]() :其他”五个选项中选择最常用的一项,将所有调查结果整理后绘制成如下不完整的条形统计图和扇形统计图,请结合统计图回答下列问题.
:其他”五个选项中选择最常用的一项,将所有调查结果整理后绘制成如下不完整的条形统计图和扇形统计图,请结合统计图回答下列问题.
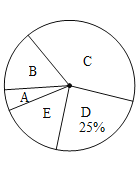
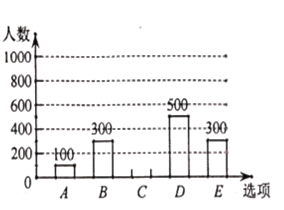
(1)本次调查中,一共调查了 名市民;扇形统计图中,![]() 项对应的扇形圆心角是_____
项对应的扇形圆心角是_____ ![]() ;
;
(2)补全条形统计图;
(3)若甲上班时从![]() 三种交通工具中随机选择一种, 乙上班时从
三种交通工具中随机选择一种, 乙上班时从![]() 三种交通工具中随机选择一种,请用列表法或画树状图的方法,求出甲、乙两人都不选
三种交通工具中随机选择一种,请用列表法或画树状图的方法,求出甲、乙两人都不选![]() 种交通工具上班的概率.
种交通工具上班的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着新冠肺炎的爆发,市场对口罩的需求量急剧增大.某口罩生产商自二月份以来,--直积极恢复产能,每日口罩生产量![]() (百万个)与天数
(百万个)与天数![]() 且
且![]() 为整数)的函数关系图象如图所示,而该生产商对口供应市场对口罩的需求量<(百万个)与天数
为整数)的函数关系图象如图所示,而该生产商对口供应市场对口罩的需求量<(百万个)与天数![]() 呈抛物线型,第
呈抛物线型,第![]() 天市场口罩缺口(需求量与供应量差)就达到
天市场口罩缺口(需求量与供应量差)就达到![]() (百万个),之后若干天,市场口罩需求量不断上升,在第
(百万个),之后若干天,市场口罩需求量不断上升,在第![]() 天需求量达到最高峰
天需求量达到最高峰![]() (百万个).
(百万个).
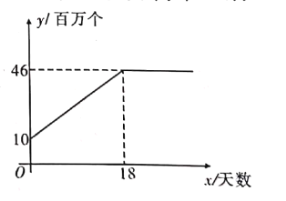
![]() 求出
求出![]() 与
与![]() 的函数解析式;
的函数解析式;
![]() 当市场供应量不小于需求量时,市民买口罩才无需提前预约,那么在整个二月份,市民无需预约即可购买口罩的天数共有多少天?
当市场供应量不小于需求量时,市民买口罩才无需提前预约,那么在整个二月份,市民无需预约即可购买口罩的天数共有多少天?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com