
 如图,在平面直角坐标系中,A($\sqrt{3}$,0),B($\sqrt{3}$,1),将△OAB绕点O逆时针旋转至△OA′B′,使点B的对应点B′,落在y轴的正半轴上.
如图,在平面直角坐标系中,A($\sqrt{3}$,0),B($\sqrt{3}$,1),将△OAB绕点O逆时针旋转至△OA′B′,使点B的对应点B′,落在y轴的正半轴上.分析 (1)根据点A、B的坐标找出OA、AB的长度,再根据特殊角的三角函数值求出∠BOA的度数,结合旋转的性质以及角的计算即可得出结论;
(2)根据点B的坐标以及旋转的性质可得出点B′的坐标,利用待定系数法即可求出直线BB′的解析式,过点A′作A′C⊥x轴于点C,根据特殊角的三角函数值找出OC、A′C的长度,进而得出点A′的坐标,再根据一次函数图象上点的坐标特征验证来验证点A′是否在直线BB′上;
(3)分别找出点A、A′在直线上时m的值,由此即可得出当直线l:y=mx与线段AA′有交点(不与端点重合)时m的取值范围.
解答 解:(1)∵A($\sqrt{3}$,0),B($\sqrt{3}$,1),
∴OA=$\sqrt{3}$,AB=1.
在Rt△OAB中,∠OAB=90°,
∴tan∠BOA=$\frac{AB}{OA}$=$\frac{\sqrt{3}}{3}$,OB=$\sqrt{O{A}^{2}+A{B}^{2}}$=2,
∴∠BOA=30°.
由旋转的性质可知:∠B′OA′=∠BOA=30°,OB′=OB=2,
∴∠BOA′=90°-∠B′OA′-∠BOA=30°.
(2)∵OB′=2,
∴B′(0,2).
设经过B、B′两点的直线所对应的一次函数表达式为y=kx+b,
将点B($\sqrt{3}$,1)、B′(0,2)代入y=kx+b中,
$\left\{\begin{array}{l}{1=\sqrt{3}k+b}\\{2=b}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=-\frac{\sqrt{3}}{3}}\\{b=2}\end{array}\right.$,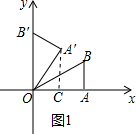
∴经过B、B′两点的直线所对应的一次函数表达式为y=-$\frac{\sqrt{3}}{3}$x+2.
过点A′作A′C⊥x轴于点C,如图1所示.
∵∠B′OA′=30°,
∴∠COA′=60°.
在Rt△OCA′中,∠OCA′=90°,OA′=OA=$\sqrt{3}$,
∴OC=OA′•cos∠COA′=$\frac{\sqrt{3}}{2}$,A′C=OA′•sin∠COA′=$\frac{3}{2}$,
∴A′($\frac{\sqrt{3}}{2}$,$\frac{3}{2}$).
当x=$\frac{\sqrt{3}}{2}$时,y=-$\frac{\sqrt{3}}{3}$×$\frac{\sqrt{3}}{2}$+2=$\frac{3}{2}$,
∴点A′在过点B、B′的直线上.
(3)当点A在直线y=mx上时,0=$\sqrt{3}$m,
∴m=0;
当点A′在直线y=mx上时,$\frac{3}{2}$=$\frac{\sqrt{3}}{2}$m,
∴m=$\sqrt{3}$.
∴若直线l:y=mx与线段AA′有交点(不与端点重合)时,m的取值范围为0<m<$\sqrt{3}$.
点评 本题考查了特殊角的三角函数值、待定系数法求函数解析式以及一次函数图象上点的坐标特征,解题的关键是:(1)根据点A、B的坐标找出∠BOA的度数;(2)利用待定系数法找出经过B、B′两点的直线解析式;(3)根据一次函数图象上点的坐标特征找出点A、A′在直线上时m的值.本题属于中档题,难度不大,解决该题型题目时,根据点的坐标利用待定系数法求出函数解析式是关键.


科目:初中数学 来源: 题型:解答题
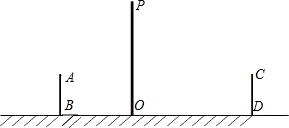 如图,是小亮晚上在广场散步的示意图,图中线段AB表示站立在广场上的小亮,线段PO表示直立在广场上的灯杆,点P表示照明灯的位置.
如图,是小亮晚上在广场散步的示意图,图中线段AB表示站立在广场上的小亮,线段PO表示直立在广场上的灯杆,点P表示照明灯的位置.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| (1)(-2)+(-7); | (2)-32-5; | (3)(-30.5)×0.2; |
| (4)12-(-18)+(-7)-15; | (5)(-$\frac{3}{4}$)×(-1$\frac{1}{2}$)×0÷(-2$\frac{1}{4}$); | (6)-9×(-11)÷3÷(-3); |
| (7)-18÷2$\frac{1}{4}$-$\frac{4}{9}$÷(-$\frac{2}{3}$); | (8)($\frac{9}{10}$-$\frac{2}{15}$+$\frac{1}{6}$)×30; | (9)1-3.9÷[1-$\frac{3}{4}$-(-0.5)]. |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 国庆节即将来临,张华高兴地看着某月的日历,发现其中有很有趣的问题,他用笔在上面画如图所示的十字框,若设任意一个十字框里的五个数为a、b、c、d、k.设中间的一个数为k,如图:试回答下列问题:
国庆节即将来临,张华高兴地看着某月的日历,发现其中有很有趣的问题,他用笔在上面画如图所示的十字框,若设任意一个十字框里的五个数为a、b、c、d、k.设中间的一个数为k,如图:试回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 两个等腰直角三角形 | B. | 各有一个角是98°的等腰三角形 | ||
| C. | 与同一个多边形相似的两个多边形 | D. | 有一个角是80°的两个等腰三角形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com