练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
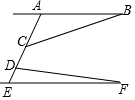
    15．如图，AB∥EF，∠BCD=135°，∠FDC=85°，则∠B+∠F的度数为（　　）
    A．38°B．40°C．55°D．60°

    分析 先根据三角形外角的性质得出∠BCD=∠B+∠BAC，∠FDC=∠F+∠DEF，再由平行线的性质得出∠BAC+∠DEF的度数，进而可得出结论．

    解答 解：∵∠BCD与∠FCD分别是△ABC与△DEF的外角，∠BCD=135°，∠FDC=85°，
    ∴∠BCD=∠B+∠BAC=135°，∠FDC=∠F+∠DEF=85°，
    ∴∠B+∠BAC+∠F+∠DEF=135°+85°=220°．
    ∵AB∥EF，
    ∴∠BAC+∠DEF=180°，
    ∴∠B+∠F=220°-180°=40°．
    故选B．

    点评 本题考查的是平行线的性质，熟知两直线平行，同旁内角互补是解答此题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    5．用适当的方法解方程组：
    （1）$\left\{\begin{array}{l}{x+y=3}\\{2x+3y=8}\end{array}\right.$；
    （2）$\left\{\begin{array}{l}{4x-3y=1}\\{3x+2y=5}\end{array}\right.$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．已知35x+3×55x+3=153x+7，则x=2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

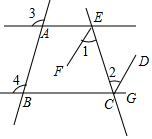    3．已知：如图，直线AE，BC被直线AB，EC所截，已知∠3=∠4，EF平分∠AEC，CD平分∠ECG，将下列证明EF∥CD的过程及理由填写完整．
    证明：∵∠3=∠4
    ∴AE∥BC（同位角相等，两直线平行）
    ∴∠AEC=∠ECG，（两直线平行，内错角相等）
    ∵EF平分∠AEC，CD平分∠ECG
    ∴∠1=$\frac{1}{2}$∠AEC，∠2=$\frac{1}{2}$∠AEC
    ∴∠1=∠2
    ∴EF∥CD（内错角相等，两直线平行）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．已知x≠1，计算
    （1-x）（1+x）=1-x2，
    （1-x）（1+x+x2）=1-x3，
    （1-x）（1+x+x2+x3）=1-x4．
    （1）观察以上各式并猜想：（1-x）（1+x+x2+…+xn）=1-xn+1（n为正整数）；
    （2）根据你的猜想计算：
    （1-2）（1+2+22+23+…+299）=1-2100；
    2+22+23+…+2n=2n+1-2．
    （x-1）（x99+x98+x97+…+x2+x+1）=x100-1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    20．一个圆柱的高为8cm，则圆柱体的体积Vcm3与底面直径Rcm的关系式为V=2πR2，当R为5cm时，V=50πcm3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．如图，已知：AB∥CD，不添加辅助线，试再添加一个条件，使∠1=∠2成立．
    要求：（1）写出两个答案；（2）选择其中一个加以证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    4．若2a=3，2b=5，则23a+2b等于675．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    5．小明在做作业时，不小心将一元一次方程2y-$\frac{1}{2}=\frac{1}{2}$y- 中的一个常数污染了．怎么办呢？小明想了一想，便翻看书后答案，此方程的解是y=-$\frac{5}{3}$，很快补好了这个常数，并迅速地完成了作业，同学们，你们能补出这个常数吗？它应是3．

    查看答案和解析>>

    同步练习册答案