
| A. | x>-3 | B. | x<-3 | C. | x>3 | D. | x<3 |
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x=2}\\{y=5}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=1}\\{y=8}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=-3}\\{y=-2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=3}\\{y=2}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 明代数学家程大位的《算法统宗》中有这样一个问题(如图),其大意为:有一群人分银子,如果每人分七两,则剩余四两;如果每人分九两,则还差八两,请问:所分的银子共有46两.(注:明代时1斤=16两,故有“半斤八两”这个成语)
明代数学家程大位的《算法统宗》中有这样一个问题(如图),其大意为:有一群人分银子,如果每人分七两,则剩余四两;如果每人分九两,则还差八两,请问:所分的银子共有46两.(注:明代时1斤=16两,故有“半斤八两”这个成语)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在Rt△ABC中,∠BAC=30°,以直角边AB为直径作半圆交AC于点D,以AD为边作等边△ADE,延长ED交BC于点F,BC=2$\sqrt{3}$,则图中阴影部分的面积为3$\sqrt{3}$-$\frac{3}{2}$π.(结果不取近似值)
如图,在Rt△ABC中,∠BAC=30°,以直角边AB为直径作半圆交AC于点D,以AD为边作等边△ADE,延长ED交BC于点F,BC=2$\sqrt{3}$,则图中阴影部分的面积为3$\sqrt{3}$-$\frac{3}{2}$π.(结果不取近似值)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 一次函数y=kx+b(k,b是常数,k≠0)的图象,如图所示,则不等式kx+b>0的解集是( )
一次函数y=kx+b(k,b是常数,k≠0)的图象,如图所示,则不等式kx+b>0的解集是( )| A. | x<2 | B. | x<0 | C. | x>0 | D. | x>2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
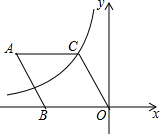 如图,在菱形ABOC中,∠A=60°,它的一个顶点C在反比例函数y=$\frac{k}{x}$的图象上,若将菱形向下平移2个单位,点A恰好落在函数图象上,则反比例函数解析式为( )
如图,在菱形ABOC中,∠A=60°,它的一个顶点C在反比例函数y=$\frac{k}{x}$的图象上,若将菱形向下平移2个单位,点A恰好落在函数图象上,则反比例函数解析式为( )| A. | y=-$\frac{{3\sqrt{3}}}{x}$ | B. | y=-$\frac{{\sqrt{3}}}{x}$ | C. | y=-$\frac{3}{x}$ | D. | y=$\frac{{\sqrt{3}}}{x}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com