
【题目】在边长为10的等边![]() 中,点
中,点![]() 从点
从点![]() 出发沿射线
出发沿射线![]() 移动,同时点
移动,同时点![]() 从点
从点![]() 出发沿线段
出发沿线段![]() 的延长线移动,点
的延长线移动,点![]() 、
、![]() 移动的速度相同,
移动的速度相同, ![]() 与直线
与直线![]() 相交于点
相交于点![]() .
.
(1)如图①,当点![]() 为
为![]() 的中点时,
的中点时,
(I)求证: ![]() ;(II)求
;(II)求![]() 的长;
的长;



(2)如图②,过点![]() 作直线
作直线![]() 的垂线,垂足为
的垂线,垂足为![]() ,当点
,当点![]() 、
、![]() 在移动的过程中,试确定
在移动的过程中,试确定![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
【答案】(1)(I)![]() (II)
(II)![]() ;(2)见解析
;(2)见解析
【解析】试题分析:
(1)I、过点P作PF∥AC交BC于点E,结合已知条件易证△PBF是等边三角形,从而可得PF=BP=CQ,由此易证△PFD≌△QCD,即可得到PD=QD;II、由△PFD≌△QCD可得DF=DC;由△PBF是等边三角形,点P是AB的中点可得BF=BP=5,由此可得FC=BC-BF=5,从而可得DC=![]() CF=
CF=![]() ;
;
(2)由点P在射线BA上移动可知,需分点P在线段AB上和点P在线段AB的延长线上两种情况讨论:I、当点P在线段AB上时,如图②,由△PFD≌△QCD可得DF=DC;由△BPF是等边三角形,PE⊥BC于点E可得BE=FE;结合BF+FC即可得到2BE+2DC=BC,从而可得BE+DC=![]() BC=
BC=![]() ;II、当点P在BA的延长线上时,如图③,过点P作过点P作PG∥AQ交BC的延长线于点G,易证△PGD≌△QCD,这样同理可得:此时BE-CD=
;II、当点P在BA的延长线上时,如图③,过点P作过点P作PG∥AQ交BC的延长线于点G,易证△PGD≌△QCD,这样同理可得:此时BE-CD=![]() BC=5.
BC=5.
试题解析:
(1)(I)如图①,过点P作PF∥AC交BC于点E,
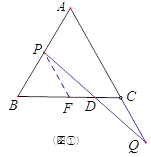
∴![]() ,
,
∴△![]() 是等边三角形,
是等边三角形,
∴![]() ,
,
又∵![]() 的运动速度相同,且同时出发,
的运动速度相同,且同时出发,
∴![]() ,
,
∴![]() ,
,
又∵∠PDF=∠QDC,
∴△PFD≌△QCD,
∴PD=QD;
(II)∵P是AB的中点,△PBF是等边三角形,
∴BP=BF=5,
∴CF=10-BF=5,
由(I)可知△PFD≌△QCD,
∴DF=DC=![]() CF=
CF=![]() ;
;
(2)如图②,
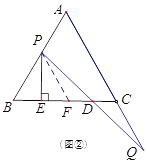
当点P在线段BA上时, ![]() =5,理由如下:
=5,理由如下:
由(I)可知:△PFD≌△QCD,
∴DF=DC,
∵PE⊥BF,
∴BE=EF,
∵BF+CF=BC,
∴2BE+2CD=BC=10,
∴BE+CD=5,即BE+CD=![]() BC=5;
BC=5;
如图③,当点P在线段BA的延长线上时, ![]() =5,理由如下:
=5,理由如下:
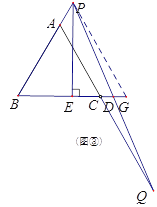
过点P作PG∥AQ交BC的延长线于点G,则∠G=∠DCQ=∠ACB=∠B=60°,∠GPD=∠CQD,
∴PG=BP,
∵点P、Q同时出发,且速度相同,
∴DQ=BP,
∴PG=QD,
∴△PGD≌△QCD,
∴DC=DG,即CG=2DC,
∵PG=PB,PE⊥BC于点E,
∴BE=GE,即BG=2BE,
∵BG-CG=BC,
∴2BE-2CD=BC,
∴BE-CD=![]() BC=5.
BC=5.


科目:初中数学 来源: 题型:
【题目】如图,在半径为5的⊙O中,弦AB=8,P是弦AB所对的优弧上的动点,连接AP,过点A作AP的垂线交射线PB于点C,当△PAB是等腰三角形时,线段BC的长为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面推理过程
如图,已知DE∥BC,DF、BE分别平分∠ADE、∠ABC,可推得∠FDE=∠DEB的理由:

∵DE∥BC(已知)
∴∠ADE= .( )
∵DF、BE分别平分∠ADE、∠ABC,
∴∠ADF=![]() ,
,
∠ABE=![]() .( )
.( )
∴∠ADF=∠ABE
∴DF∥ .( )
∴∠FDE=∠DEB. ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图所示,△AOB与△COD关于点O成中心对称,连接BC,AD.
(1)求证:四边形ABCD为平行四边形;
(2)若△AOB的面积为15 cm2,求四边形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小王购买了一套经济适用房,他准备将地面铺上地砖,地面结构如图所示.根据图中的数据(单位:m),解答下列问题:

(1)写出用含x、y的代数式表示厨房的面积是________m2;卧室的面积是________m2;
(2)写出用含x、y的代数式表示这套房的总面积是多少平方米?
(3)当x=3,y=2时,求小王这套房的总面积是多少平方米?
(4)若在(3)中,小王到某商店挑选了80cm×80cm的地砖来镶客厅和卧室,他应买多少块才够用?(结果保留整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() 的图像与
的图像与![]() 轴、
轴、![]() 轴分别相交于点
轴分别相交于点![]() 、
、![]() ,点
,点![]() 在该函数的图像上,
在该函数的图像上, ![]() 到
到![]() 轴、
轴、![]() 轴的距离分别为
轴的距离分别为![]() 、
、![]() .
.
(![]() )当
)当![]() 为线段
为线段![]() 端点
端点![]() 时,求
时,求![]() 的值.
的值.
(![]() )直接写出
)直接写出![]() 的范围,并求当
的范围,并求当![]() 时点
时点![]() 的坐标.
的坐标.
(![]() )若在线段
)若在线段![]() 上存在无数个
上存在无数个![]() 点,使
点,使![]() (
(![]() 为常数),求
为常数),求![]() 的值.
的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com