
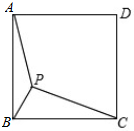
分析 (1)利用正方形的性质和旋转的性质画出P点的对应点P′,则△CBP′为所求;
(2)根据旋转的性质得BP=BP′=1,∠PBP′=90°,则可判断△PBP′为等腰直角三角形,于是PP′=$\sqrt{2}$BP=$\sqrt{2}$;
(3)由旋转的性质得CP′=AP=$\sqrt{7}$,再利用勾股定理的逆定理可证明△PP′C为直角三角形,∠PP′C=90°,而∠PP′B=45°,所以∠BP′C=135°.
解答 解:(1)如图,△CBP′为所作;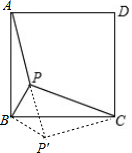
(2)∵△ABP绕B顺时针旋转90°得到△CBP′,
∴BP=BP′=1,∠PBP′=90°,
∴△PBP′为等腰直角三角形,
∴PP′=$\sqrt{2}$BP=$\sqrt{2}$;
(3)∵△ABP绕B顺时针旋转90°得到△CBP′,
∴CP′=AP=$\sqrt{7}$,
在△PP′C中,∵PC=3,P′C=$\sqrt{7}$,PP′=$\sqrt{2}$,
而($\sqrt{7}$)2+($\sqrt{2}$)2=32,
∴P′C2+PP′2=PC2,
∴△PP′C为直角三角形,∠PP′C=90°,
而∠PP′B=45°,
∴∠∠BP′C=90°+45°=135°.
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:解答题
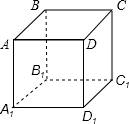 如图所示,有一放在桌面上的正方体的盒子ABCD-A1B1C1D1,在盒子外的顶点A处有一只蚂蚁,而在对角的顶点C1处有一滴蜜糖,蚂蚁应沿着正方体表面什么路径爬行,才能最快吃到蜜糖.请画出正方体的展开图及蚂蚁爬行的路线.
如图所示,有一放在桌面上的正方体的盒子ABCD-A1B1C1D1,在盒子外的顶点A处有一只蚂蚁,而在对角的顶点C1处有一滴蜜糖,蚂蚁应沿着正方体表面什么路径爬行,才能最快吃到蜜糖.请画出正方体的展开图及蚂蚁爬行的路线.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
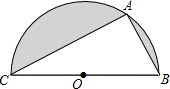 半圆内有一个直角三角形ABC,AB长为a厘米,AC长为b厘米,半圆的半径为r厘米,解答下面各题:
半圆内有一个直角三角形ABC,AB长为a厘米,AC长为b厘米,半圆的半径为r厘米,解答下面各题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
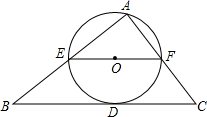 如图,⊙O过点A且与△ABC的边BC相切于D,与AB、AC分别交于E、F,EF经过圆心O,且EF∥BC,若EF=10,BD=12,求BE的长.
如图,⊙O过点A且与△ABC的边BC相切于D,与AB、AC分别交于E、F,EF经过圆心O,且EF∥BC,若EF=10,BD=12,求BE的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com