
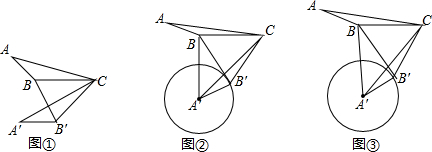
���� ��1�����ݡ�A��B��B=��A��B��C-��BB��C��ֻҪ�����BB��C���ɣ�
��2�������ۣ�ֱ��BB�����A�����У�ֻҪ֤����A��B��B=90�㼴�ɣ�������Rt��ABB���У����ù��ɶ������㼴�ɣ�
��3����ͼ���У�����+��=180��ʱ��ֱ��BB�����A�����У�ֻҪ֤����A��B��B=90�㼴�ɽ�����⣮�ڡ�CBB�������BB�䣬����Rt��A��B��B�����ù��ɶ������ɣ�
��� �⣻��1����ͼ���У��ߡ�A��B��C���ɡ�ABC��ת�õ���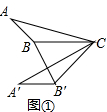
���A��B��C=��ABC=130�㣬CB=CB�䣬
���CBB��=��CB��B���ߡ�BCB��=50�㣬
���CBB��=��CB��B=65�㣬
���A��B��B=��A��B��C-��BB��C=65�㣮
��2�������ۣ�ֱ��BB�����A�����У�
���ɣ���ͼ���У��ߡ�A��B��C=��ABC=150�㣬CB=CB�䣬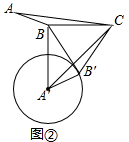
���CBB��=��CB��B���ߡ�BCB��=60�㣬
���CBB��=��CB��B=60�㣬
���A��B��B=��A��B��C-��BB��C=90�㣮
��AB���BB�䣬
��ֱ��BB�����A�����У�
������Rt��ABB���У��ߡ�AB��B=90�㣬BB��=BC=5��AB��=AB=3��
��A��B=$\sqrt{AB{��}^{2}+B��{B}^{2}}$=$\sqrt{34}$��
��3����ͼ���У�����+��=180��ʱ��ֱ��BB�����A�����У�
���ɣ��ߡ�A��B��C=��ABC=����CB=CB�䣬
���CBB��=��CB��B���ߡ�BCB��=2�£�
���CBB��=��CB��B=$\frac{180��-2��}{2}$��
���A��B��B=��A��B��C-��BB��C=��-90��+��=180��-90��=90�㣮
��AB���BB�䣬
��ֱ��BB�����A�����У�
�ڡ�CBB���У���CB=CB��=n����BCB��=2�£�
��BB��=2•nsin�£�
��Rt��A��BB����A��B=$\sqrt{BB{��}^{2}+A��B{��}^{2}}$=$\sqrt{{m}^{2}+4{n}^{2}si{n}^{2}��}$��
���� ���⿼��Բ���ۺ��⡢��ת�����ԡ����ɶ��������ߵ��ж������������ε����ʵ�֪ʶ������Ĺؼ�������������Щ֪ʶ������⣬���������ת�����ԣ������п�ѹ���⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
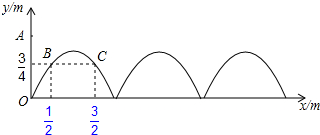
 ��ͼ��ֱ��l��y=-x+1��x�ᣬy��ֱ���A��B���㣬��P��Q��ֱ��l�ϵ��������㣬�ҵ�P�ڵڶ����ޣ���Q�ڵ������ޣ���POQ=135�㣮
��ͼ��ֱ��l��y=-x+1��x�ᣬy��ֱ���A��B���㣬��P��Q��ֱ��l�ϵ��������㣬�ҵ�P�ڵڶ����ޣ���Q�ڵ������ޣ���POQ=135�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����������ABC�ƶ���B��ʱ�뷽����ת���ȵ���A1BC1��λ�ã�AB��A1C1�ཻ�ڵ�D��AC��A1C1��BC1�ֱ��ڵ�E��F��
��ͼ����������ABC�ƶ���B��ʱ�뷽����ת���ȵ���A1BC1��λ�ã�AB��A1C1�ཻ�ڵ�D��AC��A1C1��BC1�ֱ��ڵ�E��F���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ��� | ��ѡ�ɼ�x |
| A�� | 50��x��60 |
| B�� | 60��x��70 |
| C�� | 70��x��80 |
| D�� | 80��x��90 |
| E�� | 90��x��100 |
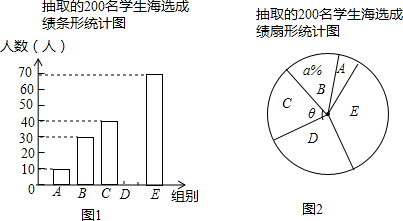
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����һ��Բ�����һ����������ɵļ����壬������ͼ�ǣ�������
��ͼ����һ��Բ�����һ����������ɵļ����壬������ͼ�ǣ�������| A�� |  | B�� |  | C�� |  | D�� | 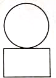 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{2016}$ | B�� | -$\frac{1}{2016}$ | C�� | 2016 | D�� | -2016 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
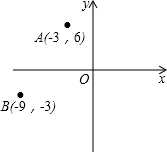 ��ͼ����ƽ��ֱ������ϵ�У���֪��A��-3��6����B��-9��-3������ԭ��OΪλ�����ģ����Ʊ�Ϊ$\frac{1}{3}$���ѡ�ABO��С�����A�Ķ�Ӧ��A��������ǣ�������
��ͼ����ƽ��ֱ������ϵ�У���֪��A��-3��6����B��-9��-3������ԭ��OΪλ�����ģ����Ʊ�Ϊ$\frac{1}{3}$���ѡ�ABO��С�����A�Ķ�Ӧ��A��������ǣ�������| A�� | ��-1��2�� | B�� | ��-9��18�� | C�� | ��-9��18����9��-18�� | D�� | ��-1��2����1��-2�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
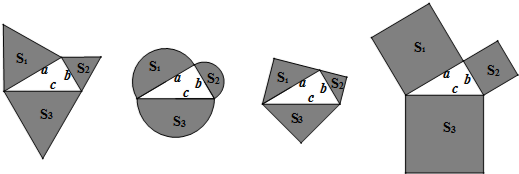
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com