
小方与同学一起去郊游,看到一棵大树斜靠在一小土坡上,他想知道树有多长,于是他借来测角仪和卷尺.如图,他在点C处测得树AB顶端A的仰角为30°,沿着CB方向向大树行进10米到达点D,测得树AB顶端A的仰角为45°,又测得树AB倾斜角∠1=75°.
(1)(5分)求AD的长. (2)(4分)求树长AB.

科目:初中数学 来源: 题型:
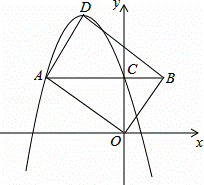
如图,已知在平面直角坐标系xOy中,O是坐标原点,抛物线y=﹣x2+bx+c(c>0)的顶点为D,与y轴的交点为C,过点C作CA∥x轴交抛物线于点A,在AC延长线上取点B,使BC=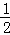 AC,连接OA,OB,BD和AD.
AC,连接OA,OB,BD和AD.
(1)若点A的坐标是(﹣4,4)
①求b,c的值;
②试判断四边形AOBD的形状,并说明理由;
(2)是否存在这样的点A,使得四边形AOBD是矩形?若存在,请直接写出一个符合条件的点A的坐标;若不存 在,请说明理由.
在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,四边形ABCD中,AC=a,BD=b,且AC⊥BD,顺次连接四边形ABCD各边中点,得到四边形 ,再顺次连接四边形
,再顺次连接四边形 各边中点,得到四边形
各边中点,得到四边形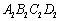 ,如此进行下去,得到四边形
,如此进行下去,得到四边形 .下列结论正确的是( )
.下列结论正确的是( )
 ①四边形
①四边形 是菱形
是菱形
②四边形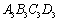 是矩形
是矩形
③四边形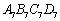 周长为
周长为
④四边形 面积为
面积为
A.①②③ B.②③④
C.①③④ D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
用一条长40cm的绳子围成一个面积为64cm2的长方形.设长方形的长为xcm,则可列方程为( )
|
| A. | x(20+x)=64 | B. | x(20﹣x)=64 | C. | x(40+x)=64 | D. | x(40﹣x)=64 |
查看答案和解析>>
科目:初中数学 来源: 题型:
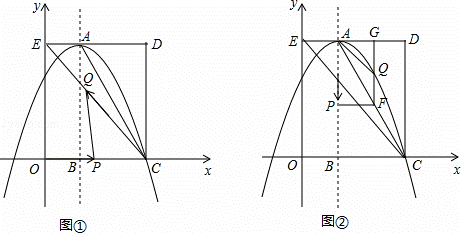
如图,在平面直角坐标系中,矩形OCDE的三个顶点分别是C(3,0),D(3,4),E(0,4).点A在DE上,以A为顶点的抛物线过点C,且对称轴x=1交x轴于点B.连接EC,AC.点P,Q为动点,设运动时间为t秒.
(1)填空:点A坐标为 ;抛物线的解析式为 .
(2)在图1中,若点P在线段OC上从点O向点C以1个单位/秒的速度运动,同时,点Q在线段CE上从点C向点E以2个单位/秒的速度运动,当一个点到达终点时,另一个点随之停止运动.当t为何值时,△PCQ为直角三角形?
(3)在图2中,若点P在对称轴上从点A开始向点B以1个单位/秒的速度运动,过点P做PF⊥AB,交AC于点F,过点F作FG⊥AD于点G,交抛物线于点Q,连接AQ,CQ.当t为何值时,△ACQ的面积最大?最大值是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com