
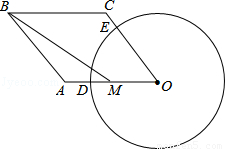
如图所示,已知四边形OABC是菱形,∠O=60°,点M是边OA的中点,以点O为圆心,r为半径作⊙O分别交OA,OC于点D,E,连接BM.若BM=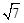 ,
,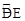 的长是
的长是 .求证:直线BC与⊙O相切.
.求证:直线BC与⊙O相切.
证明见解析
【解析】
试题分析:过点O作OF⊥BC于F,过点B作BG⊥OA于G,则四边形BGOF为矩形,OF=BG。设菱形OABC的边长为2a,先在Rt△BMG中,利用勾股定理得出BG2+GM2=BM2,即(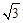 a)2+(2a)2=(
a)2+(2a)2=(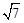 )2,求得a=1,得到OF=
)2,求得a=1,得到OF=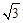 ,再根据弧长公式求出r=
,再根据弧长公式求出r=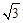 ,则圆心O到直线BC的距离等于圆的半径r,从而判定直线BC与⊙O相切。
,则圆心O到直线BC的距离等于圆的半径r,从而判定直线BC与⊙O相切。
证明:如图,过点O作OF⊥BC于F,过点B作BG⊥OA于G,则四边形BGOF为矩形,OF=BG.
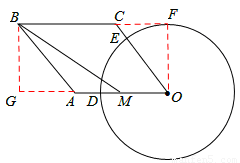
设菱形OABC的边长为2a,则AM=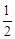 OA=a.
OA=a.
∵菱形OABC中,AB∥OC,∠COA =60°,
∴∠BAG=∠COA=60°,∠ABG=90°﹣60°=30°。
∴AG=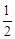 AB=a,BG=
AB=a,BG=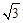 AG=
AG=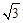 a。
a。
在Rt△BMG中,
∵∠BGM=90°,BG=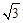 aGM=a+a=2a,BM=
aGM=a+a=2a,BM=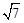 ,
,
∴BG2+GM2=BM2,即(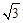 a)2+(2a)2=(
a)2+(2a)2=(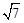 )2,解得a=1。∴OF=BG=
)2,解得a=1。∴OF=BG=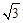 。
。
又∵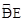 的长=
的长=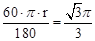 ,∴r=
,∴r=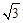 。
。
∴OF=r=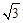 ,即圆心O到直线BC的距离等于圆的半径r。
,即圆心O到直线BC的距离等于圆的半径r。
∴直线BC与⊙O相切。


科目:初中数学 来源: 题型:
 (2013•厦门)如图所示,已知四边形OABC是菱形,∠O=60°,点M是边OA的中点,以点O为圆心,r为半径作⊙O分别交OA,OC于点D,E,连接BM.若BM=
(2013•厦门)如图所示,已知四边形OABC是菱形,∠O=60°,点M是边OA的中点,以点O为圆心,r为半径作⊙O分别交OA,OC于点D,E,连接BM.若BM=| 7 |
 |
| DE |
| ||
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图所示,已知四边形OABC是菱形,∠O=60°,点M是边OA的中点,以点O为圆心,r为半径作⊙O分别交OA,OC于点D,E,连接BM.若BM=
如图所示,已知四边形OABC是菱形,∠O=60°,点M是边OA的中点,以点O为圆心,r为半径作⊙O分别交OA,OC于点D,E,连接BM.若BM=| 7 |
 |
| DE |
| ||
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com