
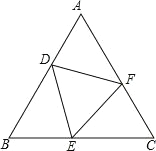
【题目】如图,△ABC 中,AB=AC,D、E、F 分别为 AB、BC、AC 上的点,且BD=CE,∠DEF=∠B.
(1)求证:∠BDE=∠CEF;
(2)当∠A=60°时,求证:△DEF 为等边三角形.
科目:初中数学 来源: 题型:
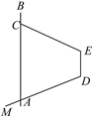
【题目】如图所示,已知射线 DM与直线AB交于点A,线段EC与直线AB交于点C,AB∥DE.
(1)当∠MAC=100°,∠BCE=120°时,把EC绕点E旋转多大角度(所求角度小于180°)时,可判定MD∥EC?请你设计出两种方案,并画出草图;
(2)若将EC绕点E逆时针旋转60°时,点C与点A恰好重合,请画出草图,并在图中找出同位角、内错角各两对(先用数字标出角,再回答).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当我们利用两种不同的方法计算同一图形的面积时,可以得到一个等式.例如,由图①,可得等式:(a+2b)(a+b)=a2+3ab+2b2.
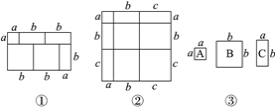
(1)由图②,写出所得的等式;
(2)利用(1)中所得到的结论,解决下面的问题: 已知a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值;
(3)如图③,琪琪用2 张A型纸片,3 张B型纸片,5 张C型纸片拼出一个长方形,那么该长方形较长的一条边长为多少.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆汽车从A地驶往B地,前三分之一路段为普通公路,其余路段为高速公路.已知汽车在普通公路上行驶的速度为60km/h,在高速公路上行驶的速度为100km/h.汽车从A地到B地共行驶了2.2h.请你根据以上信息,就该汽车行驶的“路程”或“时间”,提出一个问题: ,并列出方程,求出解.
查看答案和解析>>
科目:初中数学 来源: 题型:
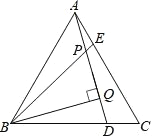
【题目】如图,在等边△ABC 中,点 D、E 分别在边 BC、AC 上,且 AE=CD,BE 与 AD 相交于点 P,BQ⊥AD 于点 Q.
(1)求证:BE=AD;
(2)若 PQ=4,求 BP 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某校综合实践活动小组的同学欲测量公园内一棵树DE的高度,他们在这棵树的正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°.已知A点的高度AB为3米,台阶AC的坡度为1: ![]() (即AB:BC=1:
(即AB:BC=1: ![]() ),且B、C、E三点在同一条直线上.请根据以上条件求出树DE的高度(侧倾器的高度忽略不计).
),且B、C、E三点在同一条直线上.请根据以上条件求出树DE的高度(侧倾器的高度忽略不计).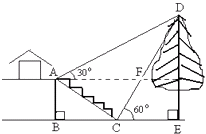
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图①,BP、CP分别平分△ABC的外角∠CBD、∠BCE,BQ、CQ分别平分∠PBC、∠PCB,BM、CN分别是∠PBD、∠PCE的角平分线.
(1)当∠BAC=40°时,∠BPC= ,∠BQC= ;
(2)当BM∥CN时,求∠BAC的度数;
(3)如图②,当∠BAC=120°时,BM、CN所在直线交于点O,直接写出∠BOC的度数.
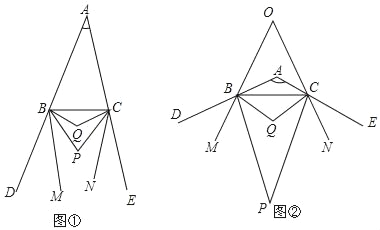
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com