
ЁОЬтФПЁПШчЭМ1ЃЌЫФБпаЮ![]() ЪЧе§ЗНаЮЃЌЖЏЕу
ЪЧе§ЗНаЮЃЌЖЏЕу![]() ДгЕу
ДгЕу![]() ГіЗЂЃЌвд
ГіЗЂЃЌвд![]() cm/sЕФЫйЖШбиБп
cm/sЕФЫйЖШбиБп![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() дШЫйдЫЖЏЕН
дШЫйдЫЖЏЕН![]() жежЙЃЛЖЏЕу
жежЙЃЛЖЏЕу![]() Дг
Дг![]() ГіЗЂЃЌвд
ГіЗЂЃЌвд![]() cm/sЕФЫйЖШбиБп
cm/sЕФЫйЖШбиБп![]() дШЫйдЫЖЏЕН
дШЫйдЫЖЏЕН![]() жежЙЃЌШє
жежЙЃЌШє![]() ЁЂ
ЁЂ![]() СНЕуЭЌЪБГіЗЂЃЌдЫЖЏЪБМфЮЊ
СНЕуЭЌЪБГіЗЂЃЌдЫЖЏЪБМфЮЊ![]() sЃЌЁї
sЃЌЁї![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ![]() cm2.
cm2. ![]() гы
гы![]() жЎМфКЏЪ§ЙиЯЕЕФЭМЯёШчЭМ
жЎМфКЏЪ§ЙиЯЕЕФЭМЯёШчЭМ![]() ЫљЪО.
ЫљЪО.
ЃЈ1ЃЉЧѓЭМ![]() жаЯпЖЮ
жаЯпЖЮ![]() ЫљБэЪОЕФКЏЪ§ЙиЯЕЪНЃЛ
ЫљБэЪОЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉЕБЖЏЕу![]() дкБп
дкБп![]() дЫЖЏЕФЙ§ГЬжаЃЌШєвд
дЫЖЏЕФЙ§ГЬжаЃЌШєвд![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЮЊЖЅЕуЕФШ§НЧаЮЪЧЕШбќШ§НЧаЮЃЌЧѓ
ЮЊЖЅЕуЕФШ§НЧаЮЪЧЕШбќШ§НЧаЮЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ3ЃЉЪЧЗёДцдкетбљЕФ![]() ЃЌЪЙ
ЃЌЪЙ![]() НЋе§ЗНаЮ
НЋе§ЗНаЮ![]() ЕФУцЛ§ЧЁКУЗжГЩ
ЕФУцЛ§ЧЁКУЗжГЩ![]() ЕФСНВПЗжЃПШєДцдкЃЌЧѓГіетбљЕФ
ЕФСНВПЗжЃПШєДцдкЃЌЧѓГіетбљЕФ![]() ЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ЁОД№АИЁПЃЈ1ЃЉ![]() ЖЮЕФКЏЪ§БэДяЪНЮЊ
ЖЮЕФКЏЪ§БэДяЪНЮЊ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЕБ![]() Лђ
Лђ![]() ЪБЃЌвд
ЪБЃЌвд![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЮЊЖЅЕуЕФШ§НЧаЮЪЧЕШбќШ§НЧаЮЃЛ
ЮЊЖЅЕуЕФШ§НЧаЮЪЧЕШбќШ§НЧаЮЃЛ
ЃЈ3ЃЉДцдк![]() КЭ
КЭ![]() ЃЌЪЙ
ЃЌЪЙ![]() НЋе§ЗНаЮ
НЋе§ЗНаЮ![]() ЕФУцЛ§ЧЁКУЗжГЩ
ЕФУцЛ§ЧЁКУЗжГЩ![]() ЕФСНВПЗжЃЎ
ЕФСНВПЗжЃЎ
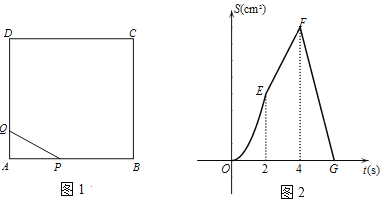
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉКЏЪ§ЭМЯѓжаЯпЖЮFGЃЌБэЪОЕуQдЫЖЏжСжеЕуDжЎКѓЭЃжЙдЫЖЏЃЌЖјЕуPдкЯпЖЮCDЩЯМЬајдЫЖЏЕФЧщаЮЃЎШчЭМ2ЫљЪОЃЌЧѓГіSЕФБэДяЪНЃЌВЂШЗЖЈtЕФШЁжЕЗЖЮЇЃЛЃЈ2ЃЉЗжРрЬжТлЃЌСаЗНГЬЧѓНтМДПЩЃЛ
ЃЈ3ЃЉЕБЕуPдкABЩЯдЫЖЏЪБЃЌPQНЋе§ЗНаЮABCDЗжГЩЁїAPQКЭЮхБпаЮPBCDQСНВПЗжЃЌШчЭМ3ЫљЪОЃЌЧѓГіtЕФжЕЃЛЕБЕуPдкBCЩЯдЫЖЏЪБЃЌPQНЋСтаЮЗжЮЊЬнаЮABPQКЭЬнаЮPCDQСНВПЗжЃЌШчЭМ4ЫљЪОЃЌЧѓГіtЕФжЕЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉгЩЬтвтЃЌПЩжЊЬтЭМ2жаЕу![]() БэЪОЕу
БэЪОЕу![]() дЫЖЏжСЕу
дЫЖЏжСЕу![]() ЪБЕФЧщаЮЃЌЫљгУЪБМфЮЊ
ЪБЕФЧщаЮЃЌЫљгУЪБМфЮЊ![]() sЃЌдђе§ЗНаЮЕФБпГЄ
sЃЌдђе§ЗНаЮЕФБпГЄ![]() cmЃЎЕу
cmЃЎЕу![]() дЫЖЏжСЕу
дЫЖЏжСЕу![]() ЫљашЪБМфЮЊЃК
ЫљашЪБМфЮЊЃК ![]() sЃЌЕу
sЃЌЕу![]() дЫЖЏжСжеЕу
дЫЖЏжСжеЕу![]() ЫљашЪБМфЮЊ
ЫљашЪБМфЮЊ![]() sЃЎ
sЃЎ
вђДЫдк![]() ЖЮФкЃЌЕу
ЖЮФкЃЌЕу![]() дЫЖЏжСЕу
дЫЖЏжСЕу![]() ЭЃжЙдЫЖЏЃЌЕу
ЭЃжЙдЫЖЏЃЌЕу![]() дкЯпЖЮ
дкЯпЖЮ![]() ЩЯМЬајдЫЖЏЃЌЧвЪБМф
ЩЯМЬајдЫЖЏЃЌЧвЪБМф![]() ЕФШЁжЕЗЖЮЇЮЊ
ЕФШЁжЕЗЖЮЇЮЊ![]() ЃЎ
ЃЎ
ЙЪ![]() ЃЌ
ЃЌ
Ёр![]() ЖЮЕФКЏЪ§БэДяЪНЮЊ
ЖЮЕФКЏЪ§БэДяЪНЮЊ![]() ЃЎ
ЃЎ
ЃЈ2ЃЉЂйШє![]() ЃЌдђ
ЃЌдђ![]() ЃЌЯдШЛВЛГЩСЂ
ЃЌЯдШЛВЛГЩСЂ
ЂкШє![]() ЃЌдђ
ЃЌдђ![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌ
ЃЌ ![]() ЃЈЩсШЅЃЉ
ЃЈЩсШЅЃЉ
ЂлШє![]() ЃЌдђ
ЃЌдђ![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌ
ЃЌ ![]() ЃЈЩсШЅЃЉ
ЃЈЩсШЅЃЉ
злЩЯЫљЪіЃЌЕБ![]() Лђ
Лђ![]() ЪБЃЌвд
ЪБЃЌвд![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЮЊЖЅЕуЕФШ§НЧаЮЪЧЕШбќШ§НЧаЮ
ЮЊЖЅЕуЕФШ§НЧаЮЪЧЕШбќШ§НЧаЮ
ЃЈ3ЃЉМйЩшДцдкетбљЕФ![]() ЃЌЪЙ
ЃЌЪЙ![]() НЋе§ЗНаЮ
НЋе§ЗНаЮ![]() ЕФУцЛ§ЧЁКУЗжГЩ
ЕФУцЛ§ЧЁКУЗжГЩ![]() ЕФСНВПЗж.взЕУе§ЗНаЮ
ЕФСНВПЗж.взЕУе§ЗНаЮ![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ![]() ЃЎ
ЃЎ
ЂйЕБЕу![]() дк
дк![]() ЩЯдЫЖЏЪБЃЌ
ЩЯдЫЖЏЪБЃЌ ![]() НЋе§ЗНаЮ
НЋе§ЗНаЮ![]() ЗжГЩЁї
ЗжГЩЁї![]() КЭЮхБпаЮ
КЭЮхБпаЮ![]() СНВПЗжЃЌШчЭМЫљЪОЃЌИљОнЬтвтЃЌЕУ
СНВПЗжЃЌШчЭМЫљЪОЃЌИљОнЬтвтЃЌЕУ![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЛ
ЃЛ
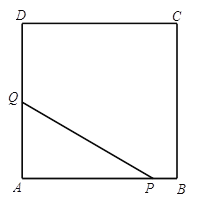
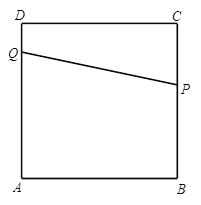
ЭМ3 ЭМ4
ЂкЕБЕу![]() дк
дк![]() ЩЯдЫЖЏЪБЃЌ
ЩЯдЫЖЏЪБЃЌ ![]() НЋе§ЗНаЮ
НЋе§ЗНаЮ![]() ЗжЮЊЬнаЮ
ЗжЮЊЬнаЮ![]() КЭЬнаЮ
КЭЬнаЮ![]() СНВПЗжЃЌШчЭМЫљЪОЃЎИљОнЬтвтЃЌЕУ
СНВПЗжЃЌШчЭМЫљЪОЃЎИљОнЬтвтЃЌЕУ![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЎ
ЃЎ
ЁрДцдк![]() КЭ
КЭ![]() ЃЌЪЙ
ЃЌЪЙ![]() НЋе§ЗНаЮ
НЋе§ЗНаЮ![]() ЕФУцЛ§ЧЁКУЗжГЩ
ЕФУцЛ§ЧЁКУЗжГЩ![]() ЕФСНВПЗжЃЎ
ЕФСНВПЗжЃЎ


 зжДЪОфЖЮЦЊЯЕСаД№АИ
зжДЪОфЖЮЦЊЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГжжГізтГЕЕФЪеЗбБъзМЃКЦ№ВНМл7дЊЃЈМДааЪЛОрРыВЛГЌЙ§3ЧЇУзЖМашИЖ7дЊГЕЗбЃЉЃЌГЌЙ§3ЧЇУзКѓЃЌУПдіМг1ЧЇУзЃЌМгЪе2.4дЊЃЈВЛзу1ЧЇУзАД1ЧЇУзМЦЃЉЃЎФГШЫГЫетжжГізтГЕДгМзЕиЕНввЕиЙВИЖГЕЗб19дЊЃЌФЧУДМзЕиЕНввЕиТЗГЬЕФзюДѓжЕЪЧЃЈ ЃЉ
A.5ЧЇУз
B.7ЧЇУз
C.8ЧЇУз
D.15ЧЇУз
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПАЫЃЈ2ЃЉАрзщжЏСЫвЛДЮОЕфРЪЖСБШШќЃЌМзЁЂввСНЖгИї10ШЫЕФБШШќГЩМЈШчБэЃЈ10ЗжжЦЃЉЃК
Мз | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
вв | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
ЃЈ1ЃЉМзЖгГЩМЈЕФжаЮЛЪ§ЪЧЗжЃЌввЖгГЩМЈЕФжкЪ§ЪЧЗжЃЛ
ЃЈ2ЃЉМЦЫуМзЁЂввЖгЕФЦНОљГЩМЈКЭЗНВюЃЌЪдЫЕУїГЩМЈНЯЮЊећЦыЕФЪЧФФвЛЖгЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЖЮЙЋТЗОВтЫуЗЂЯжЃЌдШЫйааЪЛЕФГЕСОЭЈЙ§ИУЖЮЙЋТЗЪБЃЌЫљашЪБМф![]() ЃЈhЃЉгыааЪЛЫйЖШ
ЃЈhЃЉгыааЪЛЫйЖШ![]() ЃЈkm/hЃЉТњзуЗДБШР§КЏЪ§ЙиЯЕЃЌЦфЭМЯѓЮЊШчЭМЫљЪОЕФвЛЖЮЧњЯпЃЌЧвЖЫЕуЮЊAЃЈ40ЃЌ1ЃЉКЭBЃЈmЃЌ0.5ЃЉ.
ЃЈkm/hЃЉТњзуЗДБШР§КЏЪ§ЙиЯЕЃЌЦфЭМЯѓЮЊШчЭМЫљЪОЕФвЛЖЮЧњЯпЃЌЧвЖЫЕуЮЊAЃЈ40ЃЌ1ЃЉКЭBЃЈmЃЌ0.5ЃЉ.

ЃЈ1ЃЉЧѓ![]() гы
гы![]() ЕФКЏЪ§ЙиЯЕЪНМАmЕФжЕЃЛ
ЕФКЏЪ§ЙиЯЕЪНМАmЕФжЕЃЛ
ЃЈ2ЃЉШєИУЖЮЙЋТЗЯоЫй50km/hЃЌЧѓЭЈЙ§ИУТЗЖЮашвЊЕФзюЖЬЪБМфКЭетЖЮЙЋТЗЕФГЄ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкABCDжаЃЌAEЁЂBFЗжБ№ЦНЗжЁЯDABКЭЁЯABCЃЌНЛCDгкЕуEЁЂFЃЌAEЁЂBFЯрНЛгкЕуMЃЎ 
ЃЈ1ЃЉЪдЫЕУїЃКAEЁЭBFЃЛ
ЃЈ2ЃЉХаЖЯЯпЖЮDFгыCEЕФДѓаЁЙиЯЕЃЌВЂгшвдЫЕУїЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌ ![]() ЮЊЁб
ЮЊЁб![]() ЕФжБОЖЃЌ
ЕФжБОЖЃЌ ![]() ЁЂ
ЁЂ![]() ЗжБ№ЪЧЁб
ЗжБ№ЪЧЁб![]() ЕФЧаЯпЃЌЧаЕуЮЊ
ЕФЧаЯпЃЌЧаЕуЮЊ![]() ЁЂ
ЁЂ![]() ЃЌ
ЃЌ ![]() ЁЂ
ЁЂ![]() ЕФбгГЄЯпНЛгкЕу
ЕФбгГЄЯпНЛгкЕу![]() ЃЌ
ЃЌ ![]() ,НЛ
,НЛ![]() ЕФбгГЄЯпгкЕу
ЕФбгГЄЯпгкЕу![]() .
.

ЃЈ1ЃЉЧѓжЄЃК ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШє![]() ЃЌ
ЃЌ ![]() ЃЌЧѓЁб
ЃЌЧѓЁб![]() ЕФАыОЖ.
ЕФАыОЖ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃГѕвЛФъМЖдкЩЯЮч10ЃК00ПЊеЙЁАбєЙтЬхг§ЁБЛюЖЏЃЎЩЯЮч10ЃК00етвЛЪБПЬЃЌжгБэЩЯЗжеыгыЪБеыЫљМаЕФНЧЕШгк_______ЖШЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЦНааЯпжЎМфЕФОрРыЪЧжИ(ЁЁЁЁ)
A. ДгвЛЬѕжБЯпЩЯвЛЕуЕНСэвЛжБЯпЕФДЙЯпЖЮ
B. ДгвЛЬѕжБЯпЩЯвЛЕуЕНСэвЛЬѕжБЯпЕФДЙЯпЖЮГЄЖШ
C. ДгвЛЬѕжБЯпЩЯвЛЕуЕНСэвЛЬѕжБЯпЕФДЙЯпЕФГЄЖШ
D. ДгвЛЬѕжБЯпЩЯвЛЕуЕНСэвЛЬѕжБЯпЩЯЕФвЛЕуМфЯпЖЮЕФГЄЖШ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com