
分析 (1)将点(1,-2)代入y=ax2,运用待定系数法即可求出a的值;
(2)画出函数图象.①根据函数图象找出当-1<x<0时,y随x的增大而增大;当0≤x<2时,y随x的增大而减小.再根据二次函数图象上点的坐标特征即可得出此时y的取值范围;②根据二次函数图象上点的坐标特征求出当y=-2、-4时x的值,结合函数图象即可得出x的取值范围;
(3)根据点A、B的位置不同分m<n<0、0<m<n和m<0<n三大类情况考虑,由此即可得出结论.
解答 解:(1)将点(1,-2)代入y=ax2中,
得:-2=a,
∴a=-2.
(2)依照题意画出图形,如图所示.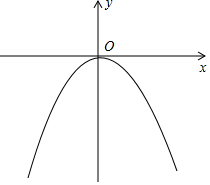
①当-1<x<0时,y随x的增大而增大;当0≤x<2时,y随x的增大而减小.
当x=-1时,y=-2;当x=0时,y=0;当x=2时,y=-8.
∴当-1<x<2时,y的取值范围是-8<y≤0.
②当y=-4时,x=±$\sqrt{2}$;当y=-2时,x=±1.
结合函数图象可知:此时x的取值范围为-$\sqrt{2}$<x<-1或1<x<$\sqrt{2}$.
故答案为:①-8<y≤0;②-$\sqrt{2}$<x<-1或1<x<$\sqrt{2}$.
(3)当m<n<0时,y1<y2;
当0<m<n时,y1>y2;
当m<0<n时分三种情况:|m|>n时,y1<y2;|m|=n时,y1=y2;|m|<n时,y1>y2.
点评 本题考查了二次函数的图象、二次函数图象上点的坐标特征以及利用待定系数法求二次函数解析式,利用待定系数法求出函数解析式并画出函数简图是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
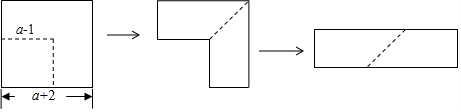
| A. | 3 | B. | 4a | C. | 6a+5 | D. | 6a+3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
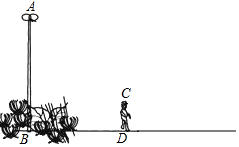 如图,小明同学利用灯光测一灯杆的高度.图中线段AB表示直立在花丛中的灯杆,线段CD表示小明,点A表示照明灯.
如图,小明同学利用灯光测一灯杆的高度.图中线段AB表示直立在花丛中的灯杆,线段CD表示小明,点A表示照明灯.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com