
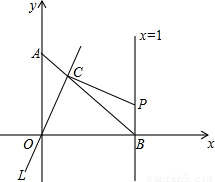
 (2008•房山区一模)如图,点A在y轴上,点B在x轴上,且OA=OB=1,经过原点O的直线l交线段AB于点C,过C作OC的垂线,与直线x=1相交于点P,现将直线L绕O点旋转,使交点C从A向B运动,但C点必须在第一象限内,并记AC的长为t,分析此图后,对下列问题作出探究:
(2008•房山区一模)如图,点A在y轴上,点B在x轴上,且OA=OB=1,经过原点O的直线l交线段AB于点C,过C作OC的垂线,与直线x=1相交于点P,现将直线L绕O点旋转,使交点C从A向B运动,但C点必须在第一象限内,并记AC的长为t,分析此图后,对下列问题作出探究: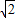 ,t=AB-BC=
,t=AB-BC=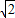 -1;
-1;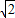 t;当t=0或1时,△PBC为等腰三角形,即P(1,1),P(1,1-
t;当t=0或1时,△PBC为等腰三角形,即P(1,1),P(1,1-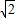 ),但t=0时,点C不在第一象限,所以不符合题意.
),但t=0时,点C不在第一象限,所以不符合题意.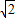 ,
,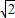 -1;
-1;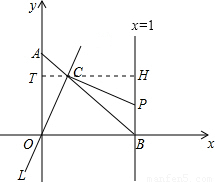 (2)OC=CP.
(2)OC=CP.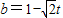 ;(0<t<
;(0<t<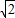 )
)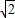 -t=|1-
-t=|1-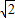 t|,
t|,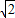 ).
).

科目:初中数学 来源:2009年云南省双柏县中考数学模拟试卷(法脿中学 郭会唐)(解析版) 题型:解答题
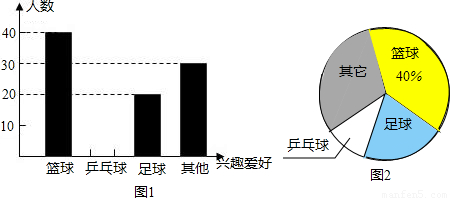
| 七年级 | 八年级 | 九年级 | |
| 学生人数 | 240 | 360 |
查看答案和解析>>
科目:初中数学 来源:2009年云南省楚雄州中考数学模拟试卷(法脿中学 郭会唐)(解析版) 题型:解答题
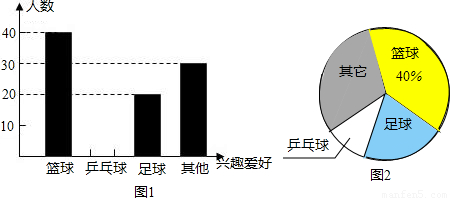
| 七年级 | 八年级 | 九年级 | |
| 学生人数 | 240 | 360 |
查看答案和解析>>
科目:初中数学 来源:2010年山东省济宁市九年级学业水平检测数学试卷(解析版) 题型:填空题
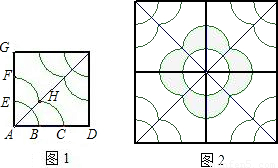
查看答案和解析>>
科目:初中数学 来源:2009年安徽省初中毕业学业模拟考试数学试卷(一)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com