
����Ŀ�����ǻ��Ͼ�����ɫ���С����ﹲ�����������Ѿ���Ϊһ��ʱ�У��������������һЩ�ﹲ���������ػ������������ǶԸ���Ʒ�Ƶ�����ѡ��������Ƴ�ͼ�ٺ�ͼ�ڵ�ͳ��ͼ��A��Ħ�ݵ�����B��ofo������C��HelloBike���������ͼ���ṩ����Ϣ������������⣺ 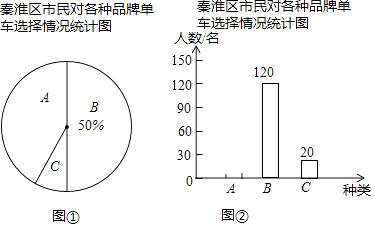
��1����ͼ���У�C������ռ���ε�Բ�ĽǶ���Ϊ�㣻
��2����ͼ�ڲ���������
��3�����ݳ������������������ij�����48�����ﹲ���������������ж�����ѡ��Ħ�ݵ�����
���𰸡�
��1��30
��2���⣺AΪ240��120��20=100��������
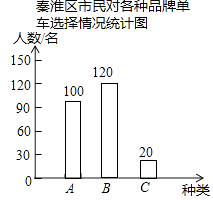 ��
��
��3���⣺48�� ![]() =20����������
=20����������
���Թ���ij�����48�����ﹲ����������������20����ѡ��Ħ�ݵ�����
����������1������B����120�ˣ���ռ�İٷֱ���50%��������õ������������Ȼ������360����Զ�Ӧ�ı������C���Ӧ���ε�Բ�ĽǵĶ�������2��������������ȥ������������������A����������Ӷ���ȫֱ��ͼ����3���������������Զ�Ӧ�ı�����⣮
�����㾫����������Ҫ����������ͳ��ͼ������ͳ��ͼ�����֪ʶ�㣬��Ҫ����������ر�ʾ������������������ռ�İٷֱȣ����Dz�������ر�ʾ��ÿ����Ŀ�ľ�����Ŀ�Լ�����ı仯�����������ر�ʾ��ÿ����Ŀ�ľ�����Ŀ�����Dz�������ر�ʾ��������������������ռ�İٷֱ��Լ�����ı仯���������ȷ�����⣮


 Ӣ�żƻ�ͬ����ʱ��Чѵ��ϵ�д�
Ӣ�żƻ�ͬ����ʱ��Чѵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������y=a��x+2����x��4����aΪ��������a��0����x������������ν���A��B���㣬��y�ύ�ڵ�C��������B��ֱ��y=�� ![]() x+b�������ߵ���һ����ΪD���ҵ�D�ĺ�����Ϊ��5��
x+b�������ߵ���һ����ΪD���ҵ�D�ĺ�����Ϊ��5��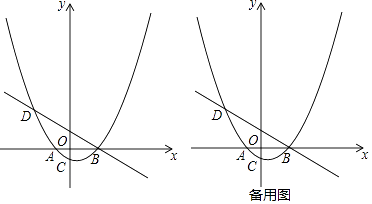
��1���������ߵĺ�������ʽ��
��2��PΪֱ��BD�·����������ϵ�һ�㣬����PD��PB�����PBD��������ֵ��
��3����FΪ�߶�BD��һ�㣨�����˵㣩������AF��һ����M�ӵ�A���������߶�AF��ÿ��1����λ���ٶ��˶���F�������߶�FD��ÿ��2����λ���ٶ��˶���D��ֹͣ������F�������Ƕ���ʱ����M�������˶���������ʱ���٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������������������������ֽ�ȫ��Ϊ�Ĵ����ֵ������������ʴ���ɼ�������������ʳƷ��320���������ʳƷ��80����
��1��������ɼ��������ʳƷ�����ټ���
��2���ּƻ����üס������ֻ�����8����һ���������������ʳƷȫ���������ֵ�������֪���ֻ��������װ����40����ʳƷ10�������ֻ�������װ�����ʳƷ��20�����������ְ��żס������ֻ���ʱ�м��ַ��������������Ƴ�����
��3���ڵڣ�2���ʵ������£�������ֻ���ÿ�����������4000Ԫ�����ֻ���ÿ�����������3600Ԫ��������Ӧѡ�����ַ�����ʹ��������٣�����������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У�DΪBC����һ�㣮
��1����ͼ�٣���Rt��ABC�У���C=90�㣬����ABC����AD�۵�����C����AB���ϣ�����ֱ�ߺ�Բ��������D����д������������ͼ�ۼ�����
��2����ͼ�ڣ�����ABC���Ź���D��ֱ���۵�����C����AB���ϵ�E����
����DE��AB������ΪE������ֱ�ߺ�Բ��������D����д������������ͼ�ۼ�����
����AB=4 ![]() ��BC=6����B=45�㣬��CD��ȡֵ��Χ�� ��
��BC=6����B=45�㣬��CD��ȡֵ��Χ�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���ACB=90�㣬D��E�ֱ���AB��AC���е㣬����DE���ӳ�����F��ʹEF=DE������AF��DC����֤���ı���ADCF�����Σ� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һλ���ߵ簮���߰����߸����ڽ���Ч����ѵľ����ݶ�֮�ϣ�Ȼ�����Ӹ˶����ݶ��Ľ�֮�䰲װ�̶��õ�֧���ߣ���������Ե�֧���߷ֱ�7��4�ף���һ����1�ף������һ���ij���ӦΪ�� ��
A. 8�� B. 9�� C. 10�� D. 12��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���B=90�㣬BC=2AB=8����D��E�ֱ��DZ�BC��AC���е㣬����DE������EDC�Ƶ�C��˳ʱ�뷽����ת������EDC��ת��A��D��E���㹲��ʱ���߶�BD�ij�Ϊ �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڽ���߶�������ϵ�����У�����������н�ƽ���ߣ������������湹��ȫ�������εĽ��˼·.�磺��ͼ1�У���![]() ��
��![]() ��ƽ����
��ƽ����![]() ��һ�㣬��
��һ�㣬��![]() ��
��![]() �ϣ���ʱ����
�ϣ���ʱ����![]() ��ȡ
��ȡ![]() ,����
,����![]() ������������ȫ�ȵ��ж�
������������ȫ�ȵ��ж�![]() ���������ȫ�������ΨS
���������ȫ�������ΨS![]() �ͨS
�ͨS![]() ,�ο�����ķ���������������⣺
,�ο�����ķ���������������⣺

��ͼ2���ڷǵȱߨS![]() �У�
�У� ![]() ,
, ![]() �ֱ���
�ֱ���![]() ��ƽ���ߣ���
��ƽ���ߣ���![]() ���ڵ�
���ڵ�![]() .��֤��
.��֤�� ![]() .
.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
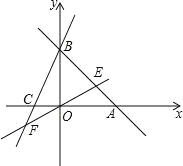
����Ŀ��ֱ��AB��y=��x+b�ֱ���x��y�ύ��A��6��0����B ���㣬����B��ֱ�߽�x�Ḻ������C����OB��OC=3��1��
(1)���B�����꣮
(2)��ֱ��BC�Ľ���ʽ��
(3)ֱ�� EF �Ľ���ʽΪy=x��ֱ��EF��AB�ڵ�E����BC�ڵ� F����֤��S��EBO=S��FBO��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com