
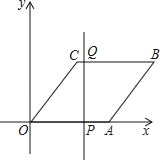
【题目】如图,在平面直角坐标系中,点A的坐标为(5,0),点B的坐标为(8,4),点C的坐标为(3,4),连接AB、BC、OC
(1)求证四边形OABC是菱形;
(2)直线l过点C且与y轴平行,将直线l沿x轴正方向平移,平移后的直线交x轴于点P.
①当OP:PA=3:2时,求点P的坐标;
②点Q在直线1上,在直线l平移过程中,当△COQ是等腰直角三角形时,请直接写出点Q的坐标.
【答案】(1)证明见解析;(2)①点P坐标为(3,0)或(15,0);②点Q坐标为:(﹣4,3),(7,1),(![]() ,
,![]() )
)
【解析】
(1)根据两点距离公式可求AO=BC=CO=AB=5,即可证四边形OABC是菱形;
(2)①分点P在线段OA上,在点A右侧两种情况讨论,根据题意可求OP的长,即可求点P的坐标;
②分三种情况讨论,根据全等三角形的判定和性质,可求点Q的坐标.
证明:(1)∵点A的坐标为(5,0),点B的坐标为(8,4),点C的坐标为(3,4),O点坐标(0,0)
∴AO=BC=5,CO=![]() =5,AB=
=5,AB=![]() =5
=5
∴AO=BC=CO=AB=5
∴四边形ABCO是菱形
(2)①当点P在线段OA上,
∵OP:PA=3:2,OP+AP=5
∴OP=3,PA=2
∴点P坐标为(3,0)
当点P在点A的右侧,
∵OP:PA=3:2,OP﹣AP=OA=5
∴OP=15,AP=10
∴点P坐标为(15,0)
②如图,当∠COQ=90°,OC=OQ时,过点C作CE⊥OA于E,则OE=3,CE=4,
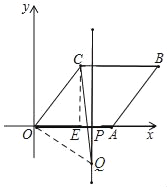
∵∠COE+∠POQ=90°,∠COE+∠OCE=90°,
∴∠OCE=∠POQ,且OC=OQ,∠CEO=∠OPQ
∴△COE≌△QOP(AAS)
∴PQ=OE=3,OP=CE=4,
∴点Q坐标(﹣4,3)
如图,当∠OCQ=90°,OC=CQ时,过点C作CE⊥OA于点E,则CE=4,OE=3,
过点Q作FQ⊥CE于点F,
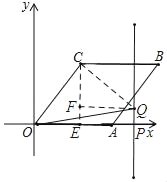
∵∠OCE+∠ECQ=90°,∠ECQ+∠CQF=90°,
∴∠OCE=∠CQF,且OC=CQ,∠OEC=∠CFQ=90°,
∴△OEC≌△CFQ(AAS)
∴CF=OE=3,FQ=CE=4,
∴EF=1,
∵QF⊥CE,CE⊥AO,PQ⊥OA
∴四边形EPQF是矩形
∴EP=FQ=4
即OP=7
∴点Q坐标为(7,1)
如图,若∠CQO=90°,CQ=OQ时,过点C作CE⊥OA于点E,则CE=4,OE=3,
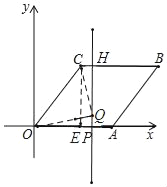
∵∠CQH+∠OQP=90°,∠PQO+∠QOP=90°,
∴∠CQH=∠QOP,且OQ=CQ,∠CHQ=∠OPQ=90°,
∴△OPQ≌△QHC(AAS)
∴OP=HQ,CH=PQ,
∵CE⊥OA,PH⊥BC,PH⊥OA
∴四边形CEPH是矩形,
∴EP=CH=PQ,HP=CE=4,
∵HQ+PQ=HP=4=OP+EP,OP﹣EP=OE=3,
∴OP=![]() ,EP=PQ=
,EP=PQ=![]()
∴点Q坐标(![]() )
)
综上所述:点Q坐标为:(﹣4,3),(7,1),(![]() )
)


科目:初中数学 来源: 题型:
【题目】在同一平面直角坐标系中,设一次函数y1=mx+n(m,n为常数,且m≠0,m≠-n)与反比例函数y2=![]() .
.
(1)若y1与y2的图象有交点(1,5),且n=4m,当y1≥5时,y2的取值范围;
(2)若y1与y2的图象有且只有一个交点,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
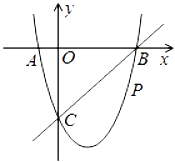
【题目】如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,﹣3)点,点P是直线BC下方的抛物线上一动点.
(1)求这个二次函数的表达式.
(2)连接PO、PC,并把△POC沿CO翻折,得到四边形POP′C,那么是否存在点P,使四边形POP′C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
(3)当点P运动到什么位置时,四边形ABPC的面积最大?求出此时P点的坐标和四边形ABPC的最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对任意一个五位正整数m,如果首位与末位、千位与十位的和均等于9,且百位为0,则称m为“开学数”.
(1)猜想任意一个“开学数”是否为![]() 的倍数,请说明理由;
的倍数,请说明理由;
(2)如果一个正整数a是另一个正整数b的立方,则称正整数a是立方数.若五位正整数m为“开学数”,记![]() ,求满足
,求满足![]() 是立方数的所有m.
是立方数的所有m.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】投资1万元围一个矩形菜园(如图),其中一边靠墙,另外三边选用不同材料建造.墙长24 m,平行于墙的边的费用为200元/m,垂直于墙的边的费用为150元/m,设平行于墙的边长为x m.
(1)设垂直于墙的一边长为y m,直接写出y与x之间的函数关系式;
(2)若菜园面积为384 m2,求x的值;
(3)求菜园的最大面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
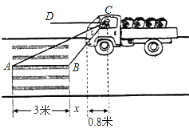
【题目】如图:一辆汽车在一个十字路口遇到红灯刹车停下,汽车里的驾驶员看地面的斑马线前后两端的视角分别是∠DCA=30°和∠DCB=60°,如果斑马线的宽度是AB=3米,驾驶员与车头的距离是0.8米,这时汽车车头与斑马线的距离x是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若 二 次 函 数 y ax bx c 的 图 象 与 x 轴 交 于 A 和 B 两 点 , 顶 点 为 C , 且b 4ac 4 ,则 ACB 的度数为()
A. 120° B. 90° C. 60° D. 30°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“千年古都,大美西安”。某校数学兴趣小组就“最想去的西安旅游景点”随机调查了本校部分学生,要求每位同学选择且只能选择一个最想去的景点,(景点对应的名称分别是:A:大雁塔 B:兵马俑 C:陕西历史博物馆 D:秦岭野生动物园 E:曲江海洋馆)。下面是根据调查结果进行数据整理后绘制出的不完整的统计图:

请根据图中提供的信息,解答下列问题:
(1)求被调查的学生总人数;
(2)补全条形统计图,并求扇形统计图中表示“最想去景点D”的扇形圆心角的度数;
(3)若该校共有800名学生,请估计“最想去景点B”的学生人数。
查看答案和解析>>
科目:初中数学 来源: 题型:
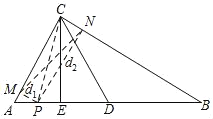
【题目】如图,点D为△ABC的AB边上的中点,点E为AD的中点,△ADC为正三角形,给出下列结论,①CB=2CE,②tan∠B=![]() ,③∠ECD=∠DCB,④若AC=2,点P是AB上一动点,点P到AC、BC边的距离分别为d1,d2,则d12+d22的最小值是3.其中正确的结论是____(填写正确结论的序号).
,③∠ECD=∠DCB,④若AC=2,点P是AB上一动点,点P到AC、BC边的距离分别为d1,d2,则d12+d22的最小值是3.其中正确的结论是____(填写正确结论的序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com