
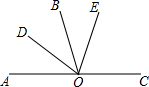
 已知,O是直线AC上一点,OD平分∠AOB,∠BOE=$\frac{1}{2}$∠EOC,∠DOE=72°,OB是∠DOE的平分线吗?说明理由.
已知,O是直线AC上一点,OD平分∠AOB,∠BOE=$\frac{1}{2}$∠EOC,∠DOE=72°,OB是∠DOE的平分线吗?说明理由. 科目:初中数学 来源: 题型:解答题
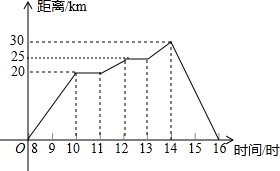 假日里,小亮和爸爸骑自行车郊游,上午8时从家出发,16时返回家中,他们离家的距离与时间的关系可用图中的折线表示.
假日里,小亮和爸爸骑自行车郊游,上午8时从家出发,16时返回家中,他们离家的距离与时间的关系可用图中的折线表示.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
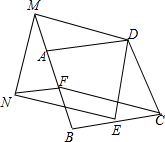 如图,四边形ABCD是正方形,点E,F分别在BC,AB上,点M在BA的延长线上,且CE=BF=AM,过点M,E分别作NM⊥DM,NE⊥DE交于N,连接NF.
如图,四边形ABCD是正方形,点E,F分别在BC,AB上,点M在BA的延长线上,且CE=BF=AM,过点M,E分别作NM⊥DM,NE⊥DE交于N,连接NF.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
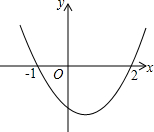 如图,抛物线y=ax2+bx+c与x轴的交点坐标是(-1,0)与(2,0),若x1,x2 (x1<x2)是方程ax2+bx+c=n(c<n<0)的两个实数根,则x1,x2的取值范围是( )
如图,抛物线y=ax2+bx+c与x轴的交点坐标是(-1,0)与(2,0),若x1,x2 (x1<x2)是方程ax2+bx+c=n(c<n<0)的两个实数根,则x1,x2的取值范围是( )| A. | x1<-1,x2>2 | B. | -1<x1<0<x2 | C. | x1<0<x2<2 | D. | -1<x1<0且0<x2<2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com