练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如果(x+y)2=1, (x-y)2=49, 求x2+y2与xy的值.

    【答案】x2+y2 =25，,xy=--12

    【解析】试题分析: 已知等式利用完全平方公式化简，相加减即可求出所求式子的值．

    试题解析:

    ∵(x+y) =x +y +2xy=1①,(xy) =x +y 2xy=49②，

    ∴①+②得：2(x +y )=50,即x +y =25；

    ①②得：4xy=48，即xy=12.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】－2a(3a－4b)= _________________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，△ABC是等边三角形，点D、E分别在边BC、AC上，∠ADE=60°．

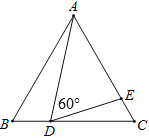
    （1）求证：△ABD∽△DCE；

    （2）如果AB=3，EC=，求DC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，ABCD中，AB⊥AC，AB=1，BC=，对角线BD、AC交于点O．将直线AC绕点O顺时针旋转分别交BC、AD于点E、F．

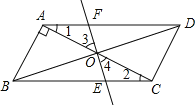
    （1）试说明在旋转过程中，AF与CE总保持相等；

    （2）证明：当旋转角为90°时，四边形ABEF是平行四边形；

    （3）在旋转过程中，四边形BEDF可能是菱形吗？如果不能请说明理由；如果能，求出此时AC绕点O顺时针旋转的角度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】分解因式4x2﹣100= ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若下列各组值代表线段的长度，以它们为边能构成三角形的是（　　）

    A. 6、13、7 B. 6、6、12 C. 6、10、3 D. 6、9、13

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，某小区在规划改造期间，欲拆除小区广场边的一根电线杆AB，已知距电线杆AB水平距离14米处是观景台，即BD=14米，该观景台的坡面CD的坡角∠CDF的正切值为2，观景台的高CF为2米，在坡顶C处测得电线杆顶端A的仰角为30°，D、E之间是宽2米的人行道，如果以点B为圆心，以AB长为半径的圆形区域为危险区域．请你通过计算说明在拆除电线杆AB时，人行道是否在危险区域内？（≈1.73）

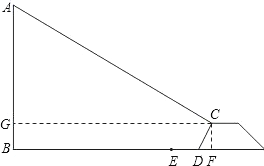
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知点A(a，3)，B(－3，b)，若点A，B关于x轴对称，则点P(－a，－b)在第____象限；若点A，B关于y轴对称，则点P(－a，－b)在第____象限．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】(3a+2)(4a2－a－1)的结果中二次项系数是( )

    A. －3 B. 8 C. 5 D. －5

    查看答案和解析>>

    同步练习册答案