
 如图,已知四边形ABCD是矩形,对角线AC、BD交于点O,CE∥BD,DE∥AC,CE与DE交于点E.
如图,已知四边形ABCD是矩形,对角线AC、BD交于点O,CE∥BD,DE∥AC,CE与DE交于点E. 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案科目:初中数学 来源: 题型:填空题
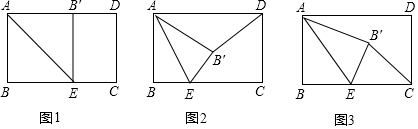
 如图,在菱形ABCD中,∠DAB=45°,AB=8,点P为线段AB上一动点,过点P作PE⊥AB交直线AD于E,沿PE将∠A折叠,点A的对称点为点F,连接EF、DF、GF,当△CDF为直角三角形时,AP=2$\sqrt{2}$或4+2$\sqrt{2}$.
如图,在菱形ABCD中,∠DAB=45°,AB=8,点P为线段AB上一动点,过点P作PE⊥AB交直线AD于E,沿PE将∠A折叠,点A的对称点为点F,连接EF、DF、GF,当△CDF为直角三角形时,AP=2$\sqrt{2}$或4+2$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
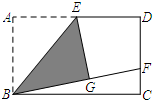 如图,在矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,延长BG交CD于点F,连接EF,若AB=3,AD=4,则△BCF的周长为( )
如图,在矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,延长BG交CD于点F,连接EF,若AB=3,AD=4,则△BCF的周长为( )| A. | $\frac{13}{3}$ | B. | $\frac{25}{3}$ | C. | 10 | D. | 12 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | 3 | D. | -3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图从一个建筑物的A处测得对面楼BC的顶部B的仰角为37°,底部C的俯角为45°,观察点与楼的水平距离AD为40m,求楼BC的高度(参考数据:sin37°≈0.60;cos37°≈0.80;tan37°≈0.75)
如图从一个建筑物的A处测得对面楼BC的顶部B的仰角为37°,底部C的俯角为45°,观察点与楼的水平距离AD为40m,求楼BC的高度(参考数据:sin37°≈0.60;cos37°≈0.80;tan37°≈0.75)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图所示,课间操时,小华、小军、小刚的位置如图,小华对小刚说:“如果我的位置用(0,0)表示,小军的位置用(2,1)表示,那么你的位置应表示为(4,3).”
如图所示,课间操时,小华、小军、小刚的位置如图,小华对小刚说:“如果我的位置用(0,0)表示,小军的位置用(2,1)表示,那么你的位置应表示为(4,3).”查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com