练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    6．四边形ABCD中，对角线AC，BD相交于点O，且OA=OC．如果再添加一个条件使得这个四边形ABCD是平行四边形，则下列条件中不能保证满足要求的是（　　）
    A．AD∥BCB．AD=BCC．AB∥CDD．OB=OD

    分析 根据平行四边形的判定定理进行解答．

    解答 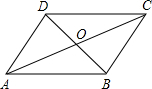解：A、通过全等三角形（△DAO≌△BCO）的对应边相等证得OD=OB，然后根据平行四边形的判定定理“对角线互相平分的四边形是平行四边形”添加条件AD∥BC．此选项不符合题意；
    B、添加条件AD=BC不能使四边形ABCD是平行四边形，此选项符合题意；
    C、通过全等三角形（△DOC≌△BOA）的对应边相等证得OD=OB，然后根据平行四边形的判定定理“对角线互相平分的四边形是平行四边形”可以添加条件AB∥CD，此选项不符合题意；
    D、根据平行四边形的判定定理“对角线互相平分的四边形是平行四边形”可以添加条件OB=OD，此选项不符合题意；
    故选B．

    点评 本题考查了平行四边形的判定，熟练掌握平行四边形的判定定理是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    16．解方程组：
    （1）$\left\{\begin{array}{l}{x-y=4}\\{4x+2y=-1}\end{array}\right.$              
    （2）$\left\{\begin{array}{l}{7x+4y=2}\\{3x-6y=24}\end{array}\right.$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    17．计算a4•a的结果等于a5．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

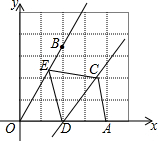    14．如图，在平面直角坐标系中，点A（4，0），点B（2，2$\sqrt{3}$），点C（2$\sqrt{3}$，2），点D（t，0）是线段OA上一动点，点A关于直线DC的对称点为E．若点E落在∠AOB的外部，则t的取值范围是0＜t＜2$\sqrt{3}$-2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    1．如图，在△ABC中，AB=AC=2$\sqrt{3}$，∠BAC=120°，点D、E都在边BC上，∠DAE=60°．若BD=2CE，则DE的长为3$\sqrt{3}$-3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．解下列不等式（组），并把解集在数轴上表示出来．
    （1）$\frac{2a-1}{3}$-4＜-$\frac{a+4}{2}$
    （2）$\left\{\begin{array}{l}{3a-2＜a+2}\\{5a+5＞2a-7}\end{array}\right.$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．下列计算正确的是（　　）
    A．$\sqrt{（\frac{1}{2}）^{2}}$=±$\frac{1}{2}$B．（$\sqrt{-\frac{1}{2}}$）2=-$\frac{1}{2}$C．$\sqrt{{3}^{2}+{4}^{2}}$=3+4D．$\sqrt{（3+4）^{2}}$=3+4

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

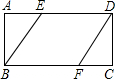    15．如图，矩形ABCD的AB=4cm，BC=7cm，在AD、BC上分别取点E、F，四边形EBFD是菱形．那么，F到直线BE的距离是（　　）
    A．3cmB．4cmC．5cmD．$\sqrt{33}$cm

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．已知：如图，在△ABC中，AD是BC边上的高，AB=13cm，AC=15cm，AD=12cm，求△ABC的面积．

    查看答案和解析>>

    同步练习册答案